TVM源语=Compute篇

【GiantPandaCV导语】使用和魔改TVM也有一段时间了，其实很多场景下，都是拿到pytorch的model，然后转成torchscript，通过relay.frontend.from_pytorch导入，然后一步一步在NVIDIA GPU上generate出网络中每个op对应的cuda code。但是，当我们的场景不在局限在神经网络的时候，比如一些由tensor构成的密集计算，就得需要通过tvm的 primitives，也即DSL来定义算法，然后通过AutoTVM或者Ansor来解决问题，当然如果要使用Ansor的话，你只需要定义好algorithm是什么样的，schedule的部分会帮你自动做，当然，如果你想得到一个custom-level的schedule，你不能完全指望Ansor能给你带来所有，所以关于tvm primitives的学习还是非常重要的。 TVM的设计思想是将“compute”和“schedule”进行decouple，那么这一片文章就将所有compute有关的primitives进行总结，下一篇将对schedule有关的primitives进行总结。

先来从最简单例子开始，一步一步深入，本篇文章会涉及如下几个例子

一维向量的加法 vector_addition
二维矩阵的乘法 gemm
卷积层的实现 conv2d

（一）Vector Addition¶

先来看第一个例子，vector_addition。在实现一个算法时，我们需要做的就是将这个算法的数学表达式写出来，然后再将其翻译成为我们熟悉的语言，交给计算机去执行。

那么vector_addition要做的其实就是：

$C[i]= A[i] + B[i]$ ,

有了这个表达式后。首先需要我们制定数组的长度为n，然后两个数组A和B，将A和B数组中对应位置元素相加放到数组C中。来看看在tvm中怎么实现？

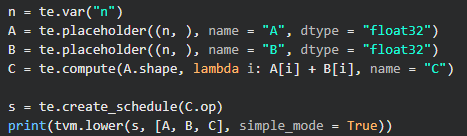
在这里插入图片描述

n表示定义的数组的长度，A，B表示分别开一个长度为n的数组，然后通过lambda表达式将A和B中每个元素的计算结果放进C中。关于te.compute其实就是你的输出结果，第一个参数A.shape表示输出矩阵的shape，lambda i:则可以理解为 for i: 0->n-1，最后通过create_schedule将生成C的过程构建出来，这个构建过程其实就是te.compute做的事情。最后通过tvm.lower将该schedule映射到IR上。我们可以通过print函数来查看：

在这里插入图片描述

是不是和平时写的C代码很像？

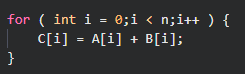
在这里插入图片描述

（二）GEMM¶

我们首先写出GEMM的数学表达式，

$D[i,j ] = \sum_{i=0}^n\sum_{j=0}^m\sum_{k=0}^{l}A[i, k] * B[k, j]+C[i,j]$

我们首先定义维度 $N\times L$ 的矩阵A，维度 $L\times M$ 的矩阵B，维度 $N\times M$ 的矩阵C。来看看TVM的实现：

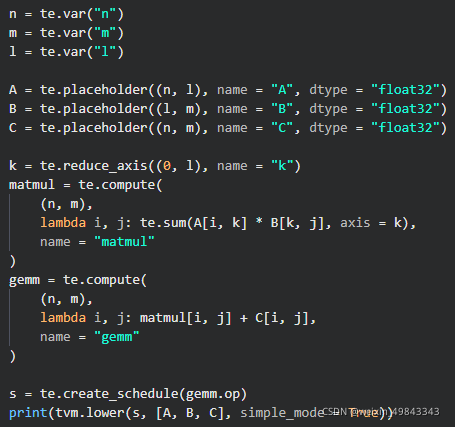
在这里插入图片描述

n,m,l分别表示矩阵的维度， $n\times l$ 的A矩阵和 $l\times m$ 的B矩阵先做矩阵乘法运算，然后在通过和 $n\times m$ 的C矩阵做相加得到最终的计算结果。先看看TVM生成的schedule是什么样的：

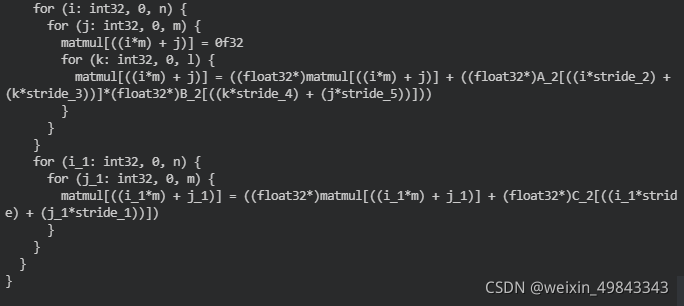
在这里插入图片描述

看到第一个te.compute是做一个三层的for-loop，也就是我们通常写两个矩阵乘法时候用到的，不难理解，这里将二维坐标的表示拆成了一维坐标的形式，其实不难理解(A[i][j] -> A'[i * width + j])，第二个te.compute生成的就是对矩阵中每个对应位置的元素的相加。

细心的同学可能会发现，这里出现了一个新的源语te.reduce_axis。该源语可以说是非常重要的一个源语，可以帮我们实现很多算法，特别有必要把这个reduce拉出来专门讲一讲。那就先讲讲reduce这个操作吧。

我一开学tvm的时候，对reduce的认识就是“约分”的意思，可能不是非常准确。就拿矩阵乘法的例子来说， $C[i,j] += A[i, k] * B[k, j]$ ，可以发现，在经过运算后，等号右边的表达式有(i, j, k)这三个维度变成了仅仅只有(i, j)这两个维度。当然，这样做的好处是什么？试想有一个10层for-loop的程序来对一组变量进行操作 $A[i_0, i_1, ..., i_9]$ ，最终我只希望得到一个6维的向量，那么其中有4层的for-loop就可以被reduce掉。可能矩阵的乘法并不能看到他的优点，当我们要去写一个非常简单的卷积的时候，就可以看到reduce带来的优势了。这里用一个数字图像处理中的简单卷积举例子(input feature map的channel是1， output feature map的channel也是1)，算法的描述如下所示，input是一个 $n*n$ 的卷积，卷积核的大小是 $5*5$ ，output是通过te.compute计算得到。

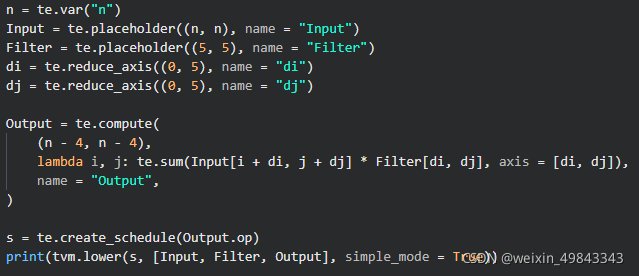
在这里插入图片描述

来讲讲上面的写法，这是一个非常naive的卷积实现，不涉及到padding的操作，直接拿着 $5*5$ 的kernel在一个 $n*n$ 的单通道图像上进行滤波，通过数学推导，我们可以到针对单一窗口的运算结果：

$Output[d_i,d_j] = \sum_{d_i=0}^{5}\sum_{d_j=0}^{5}Input[d_i, d_j] * Filter[d_i,d_j]$

当窗口滑动起来后，就得去改变(i, j)的值了，我们只需要在 $input[d_i, d_j]$ 的基础上添加坐标(i, j)就行。

那么表达式就被更新为:

$Output[i,j] = \sum_{i=0}^n\sum_{j=0}^m\sum_{d_i=0}^{5}\sum_{d_j=0}^{5}Input[i + d_i, j + d_j] * Filter[d_i,d_j]$

因为最终得到的Output是一个(n-4) * (n-4)的数组，那么我们就可以使用reduce来对 $d_i$ 和 $d_j$ 进行操作。

其实reduce还是有很多操作需要学习的，这里在介绍一下te.compute同时接受多个输入。

来看下面的例子，比如我有两个数组 $A_0[i,j], A_1[i,j]$ ,那么 $B_0[i,j] = A_0[i, j]*3$ , $B_1[i,j] = A_1[i,j] + 5$ ，A数组具有相同的维度，长度都为n。那么如果放到C/C++的实现，就是写两层循环循环分别给 $B_0，B_1$ 数组赋值。那么，用TVM的DSL该怎么实现呢？

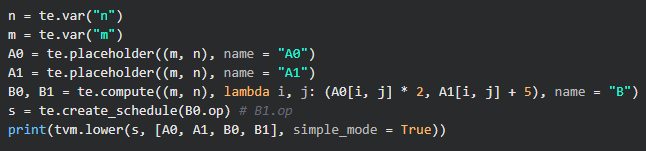
在这里插入图片描述

其实很简单，看看生成的schedule是什么样子？

在这里插入图片描述

B0,B1的计算都被统一到两个for-loop中了，而不是分开运算。当然，当我们用下面的写法时，

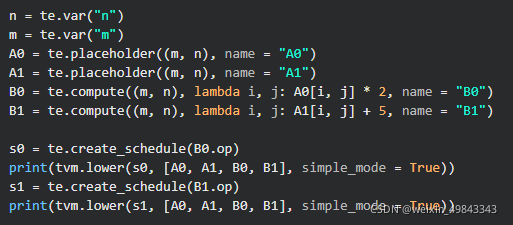
在这里插入图片描述

那么相对应生成的schedule应该如下所示：

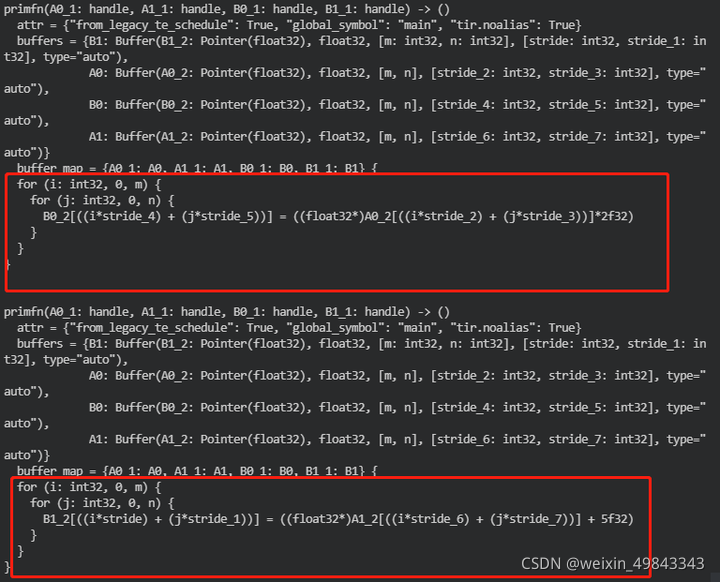
在这里插入图片描述

这种实现实际是不高效的，因为对于维度相同的for-loop，我们在写code的时候，都是尽量将他们放在一起。至于这样的优化是不是适用于所有情况，确实值得商榷。

(三) 卷积层的实现¶

前面在介绍GEMM例子的时候，我们使用了一个非常简单的单通道图像和滤波器做卷积的例子。然而在深度学习中使用卷积的时候，我们都是使用多个input channel的input feature map和多个output channel的feature map，然后对input feature map进行padding到合适大小，然后进行卷积操作。我们来规范下conv2d的参数

data layout：NCHW

input feature map：[128, 256, 64, 64]

filter: [512, 256, 3, 3, 1, 1] (pad: 1，stride:1)

解释下，[128, 256, 64, 64]表示的是，输入的特征图的batch为128，input channel是256，并且输入进来的维度是64*64的。[512, 256, 3, 3]表示的是卷积核的参数，output channel是512，input channel是256，必须和input feature map的输入channel保持一致，然后3乘3表示的是kernel size，pad为1，stride也为1。

OK，有了这些参数介绍后，我们就可以很容易用TVM的DSL构建一套卷积算法的描述了。

卷积第一步要做的就是给input feature map进行pad操作，使得其pad后的input feature map在经过卷积后，output feature map的尺寸和input feature map的尺寸相同 $pad = \frac{kernel\_size - 1}{2} )$ ，先来讲讲补0操作，补0操作在传统数字图像处理中用的也是非常多的。

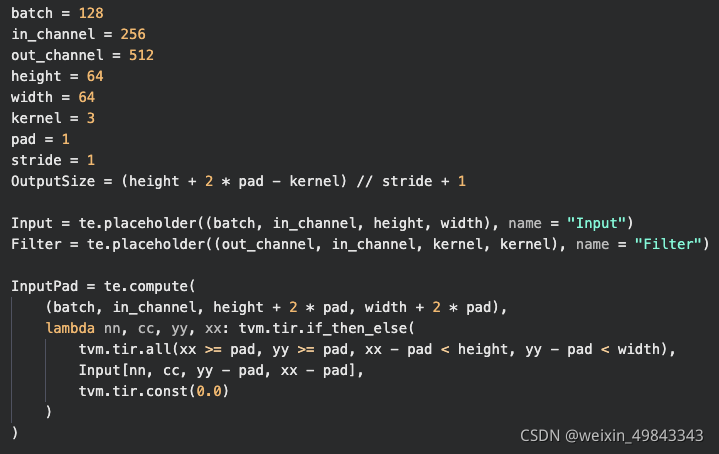
在这里插入图片描述

补0操作，其实就是在原始的input feature map的上，下，左，右四个边各补了一圈0 (pad=1)，那么原先input feature map中对应的Input[0][0]的元素在after padding后就变成了InputPad[1][1]，以此类推，在y方向和x方向的[1, 64]出对应的就是原先的Input(64 * 64)。这样，我们就可以知道InputPad后哪些element为0，哪些element为1，对应生成的schedule如下所示：

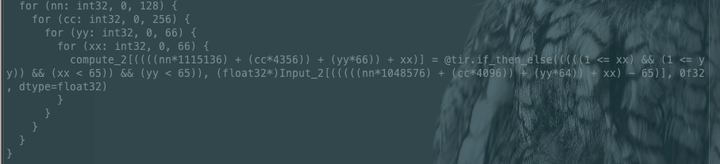
在这里插入图片描述

补完边后，接下来就是来做conv2d操作了，由于我们的data layout采用的是 NCHW，所以在用TVM的DSL实现的过程中，lambda表达式的循环顺序应该是batch->in_channel->height->width。结合前面讲过的一维卷积的例子，针对Filter的三个维度(out_channel, kernel_size, kernel_size)使用te.reduce_axis操作。

在这里插入图片描述

一个简单的conv2d算法可以表示成7层for-loop，那么通过三个reduce_axis操作以后，就会产生剩下的4层for-loop。上图算法中，B表示batch_size, K表示out_channel, C表示In_channel,Y表示Height, X表示Width, Fy和Fx分别表示的是kernel_size。那么使用TVM的DSL描述的卷积如下所示：

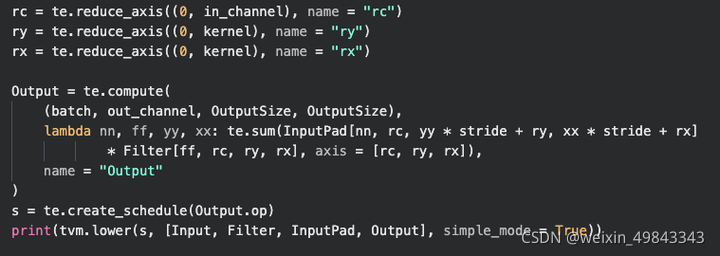
在这里插入图片描述

对应的schedule如下所示：

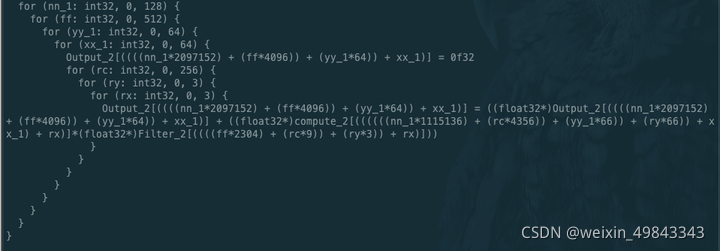
在这里插入图片描述

(四)总结¶

总结一下，TVM的DSL其实包含很多内容，和我们平时写序列形式的code的style不太一样，这种写法更偏向functional programming的模式，当然这样写的好处也很明显，通过lambda表达式和reduce_axis的组合，将for-loop的形式hidden起来，增加大家对于算法的理解，从而让compiler的后端能更好的优化前端通过DSL定义的for-loop。

本文总阅读量次