【GiantPandaCV导语】计算Armv7a架构理论gflops以及自己写的某个算法的gflops的方法，另外提供了一个脚本可以显示native版矩阵乘法各个尺寸对应的gflops。

1. 前言¶

之前一直在写一些算法怎么优化，包括算法逻辑甚至是更加底层一些的文章，但是测试工作都做得比较随意，也就是粗略的比较时间。最近准备学习一下矩阵乘法的优化，觉得这种比较方式实际上是看不出太多信息的，比如不知道当前版本的算法在某块指定硬件上是否还存在优化空间。因此，这篇文章尝试向大家介绍另外一个算法加速的评判标准，即算法的浮点峰值（gflops）。

gflops代表计算量除以耗时获得的值。

之前高叔叔发了一篇文章教会我们如何计算硬件的浮点峰值（https://zhuanlan.zhihu.com/p/28226956），高叔叔的开源代码是针对x86架构的。然后，我针对移动端(ArmV7-a架构)模仿了一下，在测出硬件的浮点峰值之后，手写了一个Native版的矩阵乘法并计算这个算法的gflops，以判断当前版本的算法离达到硬件浮点峰值还有多少优化空间。

2. Cortex-A53 硬件浮点峰值计算¶

详细原理请查看：浮点峰值那些事。这里再截取一下计算浮点峰值的操作方法部分：

来自https://zhuanlan.zhihu.com/p/28226956

所以参考这一方法，即可在移动端测出浮点峰值，首先写出测试的核心代码实现，注意gflops的计算方法就是用计算量除以程序耗时：

#include <time.h>
#include <stdio.h>

#define LOOP (1e9)
#define OP_FLOATS (80)

void TEST(int);

static double get_time(struct timespec *start,
                       struct timespec *end) {
    return end->tv_sec - start->tv_sec + (end->tv_nsec - start->tv_nsec) * 1e-9;
}



int main() {
    struct timespec start, end;
    double time_used = 0.0;

    clock_gettime(CLOCK_MONOTONIC_RAW, &start);

    TEST(LOOP);

    clock_gettime(CLOCK_MONOTONIC_RAW, &end);

    time_used = get_time(&start, &end);
    printf("perf: %.6lf \r\n", LOOP * OP_FLOATS * 1.0 * 1e-9 / time_used);
}

注意这里的TEST是使用了纯汇编实现，即test.S文件，代码如下，为什么一次循环要发射10条vmla.f32指令，上面截取的计算方法部分讲的很清楚，这个地方也可以自己多试几组值获得更加精细的硬件FLOPs：

.text
.align 5

.global TEST

TEST:

.loop2:
    vmla.f32 q0, q0, q0
    vmla.f32 q1, q1, q1
    vmla.f32 q2, q2, q2
    vmla.f32 q3, q3, q3
    vmla.f32 q4, q4, q4
    vmla.f32 q5, q5, q5
    vmla.f32 q6, q6, q6
    vmla.f32 q7, q7, q7
    vmla.f32 q8, q8, q8
    vmla.f32 q9, q9, q9

    subs r0,r0,    #1
    bne .loop2

我在Cortex-A53上测试了单核的浮点峰值，结果如下：

峰值测试

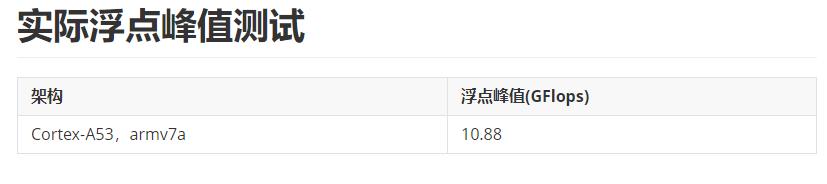
然后大概知道了硬件的浮点峰值，我们在优化自己的算法时就至少心中有数了。

3. 实现Native矩阵乘法，记录浮点峰值¶

接着，我们参考https://github.com/flame/how-to-optimize-gemm来实现一个Native版的矩阵乘法，即A矩阵的一行乘以B矩阵的一列获得C矩阵的一个元素（计算量为2 * M * N * K），并统计它的运算时间以计算gflops，另外为了发现矩阵乘法的gflops和矩阵尺寸的关系，我们将各个尺寸的矩阵乘法的gflops写到一个txt文件里面，后面我们使用Python的matplotlib库把这些数据画到一张图上显示出来。首先实现不同尺寸的矩阵乘法：

#define A( i, j ) a[ (i)*lda + (j) ]
#define B( i, j ) b[ (i)*ldb + (j) ]
#define C( i, j ) c[ (i)*ldb + (j) ]
// gemm C = A * B + C
void MatrixMultiply(int m, int n, int k, float *a, int lda, float *b, int ldb, float *c, int ldc)
{
    for(int i = 0; i < m; i++){
        for (int j=0; j<n; j++ ){    
            for (int p=0; p<k; p++ ){      
                C(i, j) = C(i, j) + A(i, p) * B(p, j);
            }
        }
    }
}

测试和统计FLOPs部分的代码比较长，就贴一点核心部分吧，完整部分可以到github获取（https://github.com/BBuf/ArmNeonOptimization/tree/master/optimize_gemm）：

// i代表当前矩阵的长宽，长宽都等于i
for(int i = 40; i <= 800; i += 40){
       m = i;
       n = i;
       k = i;
       gflops = 2.0 * m * n * k * 1.0e-09;
       lda = m;
       ldb = n;
       ldc = k;
       a = (float *)malloc(lda * k * sizeof(float));
       b = (float *)malloc(ldb * n * sizeof(float));
       c = (float *)malloc(ldc * n * sizeof(float));
       prec = (float *)malloc(ldc * n * sizeof(float));
       nowc = (float *)malloc(ldc * n * sizeof(float));
       // 随机填充矩阵
       random_matrix(m, k, a, lda);
       random_matrix(k, n, b, ldb);
       random_matrix(m, n, prec, ldc);

       memset(prec, 0, ldc * n * sizeof(float));

       copy_matrix(m, n, prec, ldc, nowc, ldc);

       // 以nowc为基准，判断矩阵运行算结果是否正确
       MatrixMultiply(m, n, k, a, lda, b, ldb, nowc, ldc);

       // 循环20次，以最快的运行时间为结果
       for(int j=0; j < 20; j++){

           copy_matrix(m, n, prec, ldc, c, ldc);

           clock_gettime(CLOCK_MONOTONIC_RAW, &start);

           MatrixMultiply(m, n, k, a, lda, b, ldb, c, ldc);

           clock_gettime(CLOCK_MONOTONIC_RAW, &end);

           time_tmp = get_time(&start, &end);

           if(j == 0)
               time_best = time_tmp;
           else
               time_best = min(time_best, time_tmp);
       }

       diff = compare_matrices(m, n, c, ldc, nowc, ldc);

       if(diff > 0.5f || diff < -0.5f){
           exit(0);
       }

       printf("%d %le %le \n", i, gflops / time_best, diff);
       fflush(stdout);

       free(a);
       free(b);
       free(c);
       free(prec);
       free(nowc);
}
printf("\n");
fflush(stdout);

在编译之后运行时只需要新增一个重定向命令，即可获得记录了矩阵大小和GFlops的txt文件，例： ./unit_test >> now.txt，注意now.txt需要自己先创建，并保证它有可写的权限。

接下来我们使用下面的脚本将now.txt用图片的方式显示出来，并将图片保存到本地：

import matplotlib.pyplot as plt
import numpy as np

def solve(filename):
    f = open(filename)
    sizes = [40]
    times = [0.0]
    title = 'origin'
    while True:
        line = f.readline()
        if line:
            slices = line.split(" ")
            if len(slices) <= 2:
                break;
            size = int(slices[0])
            time = float(slices[1])
            sizes.append(size)
            times.append(time)
    return title, sizes, times

if __name__ == '__main__':
    plt.xlabel('size')
    plt.ylabel('gflops')
    t, x, y = solve('now.txt')
    plt.plot(x, y, label=t)
    plt.legend()
    plt.savefig('origin.png')
    plt.show()

我们来看一下结果：

测试结果

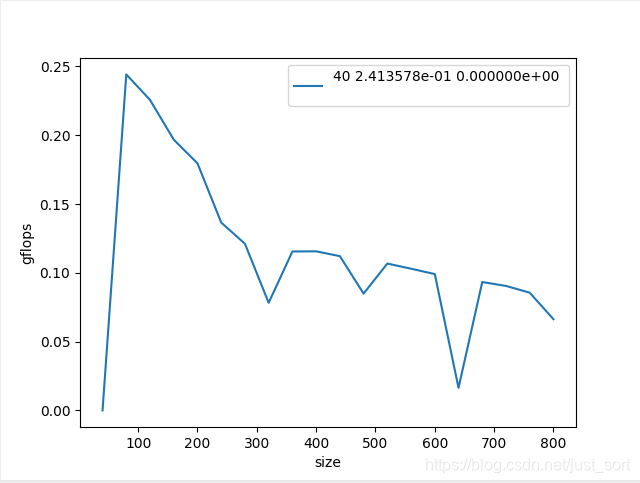
从这张图可以看到，在矩阵长宽取100的时候可以达到最高的gflops大概是0.25gflops，相对硬件的理论浮点峰值只有2-3%，所以此算法的优化空间还是非常巨大的，接下来我们就可以使用如减少乘法次数，内存对齐，分块等策略去改进这个算法获得更好的gflops。这样，我们在算法优化的过程中就可以更加直观的看到算法的性能。

4. 小结¶

这篇文章只是矩阵优化部分的开篇，主要是受到高叔叔的文章启发给对移动端或者PC端感兴趣的同学提供一个gflops的计算实例，并提供一个将gflops更加直观显示的脚本工具，希望对大家有用。

5. 参考¶

本文总阅读量次