移动端arm cpu优化学习笔记第2弹--常量阶时间复杂度中值滤波
本文复现的文章:
Median Filtering in Constant Time
该文章C++复现代码:
最近在复现 Side window 中值滤波的时候就在思考中值滤波能怎么优化,直观上看中值滤波好像没什么可优化的点,因为中值滤波需要涉及到排序,而且半径越大,排序的耗时也越大。那么中值滤波能否进一步加速呢?或者像均值滤波一样,可以不受滤波半径的影响呢?
答案是能!这篇博客就是记录了我是怎么去优化中值滤波的实践过程。而前面的3小节都是介绍我自己尝试的优化思路,最后一节才是讲本文标题提到的常量阶时间复杂度中值滤波的实现思路,想直接看其实现思路的读者可以跳到最后一小节。
1、一般中值滤波的实现
一开始能想到的中值滤波最直观的实现就是,把每个滤波窗口的内的值放进一个数组里面,然后排序,排序结果的排中间的值就是滤波结果。下面给出中值滤波的一般实现的示例代码(下面展示的所有代码只是为了用于说明,不保证能运行,实际代码以github上的代码为准):
median_filter(const float *input,
const int radius,
const int height,
const int width,
float *output) {
int out_idx = 0;
for (int h = 0; h < height; ++h) {
const int h_lower_bound = std::max(0, h - radius);
const int h_upper_bound = std::min(height - 1, h + radius);
const int h_interval = h_upper_bound - h_lower_bound + 1;
for (int w = 0; w < width; ++w) {
const int w_left_bound = std::max(0, w - radius);
const int w_right_bound = std::min(width - 1, w + radius);
const int arr_len = h_interval * (w_right_bound - w_left_bound + 1);
int idx = 0;
for (int i = h_lower_bound; i <= h_upper_bound; ++i) {
const int h_idx = i * width;
for (int j = w_left_bound; j <= w_right_bound; ++j) {
m_cache[idx ++] = input[h_idx + j];
}
}
sortArr(m_cache.data(), arr_len);
output[out_idx ++] = m_cache[arr_len / 2];
}
}
}
排序函数sortArr的实现函数,这是实现的是选择排序法:
static void sortArr(float *arr, int len) {
const int middle = len / 2;
for (int i = 0; i <= middle; ++i) {
float min = arr[i];
int min_idx = i;
for (int j = i + 1; j < len; ++j) {
if (min > arr[j]) {
min_idx = j;
min = arr[j];
}
}
// swap idx i and min_idx
float tmp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = tmp;
}
}
这里有个 小技巧 是,实现排序函数的时候因为我们只是为了求中值, 所以只需计算出前一半的有序元素即可 ,比如数组:
132, 45, 8, 1, 9, 100, 34
一般是全部排完得到:
1, 8, 9, 34, 45, 100, 132
中值就是34,但其实外部循环迭代只需要迭代到原来的一半(7 / 2)= 3 就行了就可停止了,下面看下选择排序中间每一步结果:
第0步,1和132交换:
132 , 45, 8, 1 , 9, 100, 34 -> 1, 45, 8, 132, 9, 100, 34
第1步,8和45交换:
1, 45 , 8 , 132, 9, 100, 34 -> 1, 8, 45, 132, 9, 100, 34
第2步,9和45交换:
1, 8, 45 , 132, 9 , 100, 34 -> 1, 8, 9, 132, 45, 100, 34
第3步,34和132交换:
1, 8, 9, 132 , 45, 100, 34 -> 1, 8, 9, 34, 45, 100, 132
到这一步就可停止,因为中值已经得到了,不过刚好这个例子是排到这一步就全部排好了而已。
然后看下这个最普通的实现在手机上的耗时,测试机型是华为P30(麒麟980),下面所有实验设置输入分辨率都是512x512,滤波半径大小从1到5,耗时跑30次取平均:

可以看到性能很一般,而且随着半径增加耗时也急剧增加。下面来看下第一版的优化,首先可以优化的点就是计算的数据类型。
2、第一版优化,float数据类型改uint16_t
因为一般我们处理图像的数据像rgb类型的数据其起取值范围是[0 ~ 255],这时候其实完全不需要用float来存储,用uint16_t类型就足够了,中间计算也是全部用uint16_t替换,完整代码:
这样子简单改一下数据类型之后,我们来看下其耗时:

可以看到就是简单改下运算数据类型,其运行耗时就可以下降不少。
3,第二版优化,简单利用并行计算指令
这版优化其实非常的暴力,就是既然每个窗口单次排序这样子太慢,那么就利用并行计算一次同时计算8个窗口的排序结果,下面是示例代码:
#if defined(USE_NEON_INTRINSIC) && defined(__ARM_NEON)
int neon_arr_len = h_interval * (w_end - w_start + 1) * 8;
for (int w = w_second_loop_start; w < remain_start; w += 8) {
const int w_left_bound = std::max(0, w + w_start);
const int w_right_bound = std::min(width - 1, w + w_end);
int idx = 0;
for (int i = h_lower_bound; i <= h_upper_bound; ++i) {
const int h_idx = i * width;
for (int j = w_left_bound; j <= w_right_bound; ++j) {
for (int q = 0; q < 8; ++q) {
m_cache[idx ++] = input[h_idx + j + q];
}
}
}
sortC4ArrNeon(m_cache.data(), neon_arr_len);
for (int i = 0; i < 8; ++i) {
m_out_buffer[out_idx ++] = m_cache[(neon_arr_len / 8 / 2) * 8 + i];
}
}
#endif
完整代码见:
从代码上可以看到,因为用的是uint16_t类型的数据,所以可以一次处理8个窗口,相当于把从左到右8个窗口内的数据打包成C8的结构,然后看下排序函数的改动:
#if defined(USE_NEON_INTRINSIC) && defined(__ARM_NEON)
static void sortC4ArrNeon(uint16_t *arr, int len) {
const int actual_len = len / 8;
const int middle = actual_len / 2;
uint16_t *arr_ptr = arr;
for (int i = 0; i <= middle; ++i) {
uint16x8_t min = vld1q_u16(arr_ptr);
uint16x8_t min_idx = vdupq_n_u16(i);
uint16_t *inner_arr_ptr = arr_ptr + 8;
for (int j = i + 1; j < actual_len; ++j) {
uint16x8_t curr = vld1q_u16(inner_arr_ptr);
uint16x8_t curr_idx = vdupq_n_u16(j);
uint16x8_t if_greater_than = vcgtq_u16(min, curr);
min = vbslq_u16(if_greater_than, curr, min);
min_idx = vbslq_u16(if_greater_than, curr_idx, min_idx);
inner_arr_ptr += 8;
}
// swap idx i and min_idx
for (int q = 0; q < 8; ++q) {
float tmp = arr[min_idx[q] * 8 + q];
arr[min_idx[q] * 8 + q] = arr[i * 8 + q];
arr[i * 8 + q] = tmp;
}
arr_ptr += 8;
}
}
#endif // __ARM_NEON
其实代码上看主体框架改动不大,还是采用选择排序法,不过如何利用neon intrinsic并行计算指令,同时对8个窗口内的数据进行排序呢?借助 vcgtq 和 vbslq 这两个指令就可以做到。
vcgtq 表示将第一个参数内的数组元素与第二个参数对应元素比较,如果第一个数组的元素,大于等于对应第二个数组的对应元素,则结果对应位置会置为1,否则为0。
vbslq 指令有三个输入,第一个输入可以看做是判断条件,如果第一个输入的元素位置是1则结果的对应的位置就取第二个输入的对应位置,否则从第三个输入对应位置取值。其实这和mxnet的where操作子很像。
然后一次循环迭代完了之后,min_idx 数组就包含了这8个窗口当前迭代的各自最小值的位置。
ok,我们接着来看下这版的耗时:

可以看到用了neon加速之后,耗时减少了很多,大概是3~4倍的提速。
4,第三版优化,算法上的改进
经过前面的铺垫,终于到了本文的重点部分。如何让中值滤波的耗时不受滤波半径的影响,其实本质来说就是 改变一下计算滤波窗口内中值的思路,不再采用排序,而是 采用统计直方图的方式,因为一般图像数据rgb取值范围就是[0~255],那么求一个窗口内的的中值完全可以采统计这个窗口内的长度是256的直方图,然后中值就是从左到右遍历直方图,累加直方图内每个bin内的值,当求和结果大于等于窗口内元素个数的一半,那么这个位置的索引值就是这个窗口的中值。
不过这也不能解决滤波半径增大的影响,那么如何去除半径的影响呢,本文开头提到的这篇 “Median Filtering in Constant Time ” 文章里面引入了 列直方图 的方法,也就是除了统计滤波窗口的直方图,还对于图像的每一列,都初始化一个长度是256的直方图,所以 滤波图像太宽的话需要的内存消耗也会更多 。
然后不考虑边界部分,对于中间部分的滤波窗口,其直方图不需要重新统计,只需要减去移出窗口的列直方图,然后加上新进来的列直方图即可,然后再计算中值,这三步加起来时间复杂度不会超过O(256*3),不受滤波半径影响,所以在行方向上是常量阶时间复杂度。
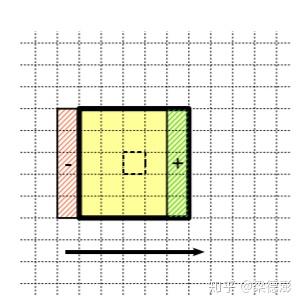
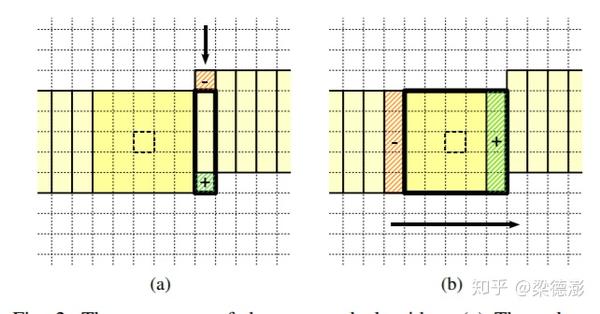
然后列方向就是同样的,列直方图在往下一行移动的时候也是采用同样方法更新,减去上一行和加上下一行的值,然后这样子列方向上也不受滤波半径影响了。
论文里采用的计算方式,当从左到右滤波的时候,第一次用到列直方图的时候才去更新列直方图,而我在实现的时候是移动到新的一行从头开始滤波之前,首先更新所有的列直方图,然后再计算每个滤波窗口的中值。而且我在申请直方图缓存的时候是所有直方图都放在同一段缓存内。
之后来看下这一版的耗时:

可以看到耗时很稳,基本不受滤波半径影响,不过由于需要涉及到直方图的计算,在滤波窗口比较小的时候,这个算法相对于直接算是没有优势的,但是当滤波窗口大于等于3的时候,其优势就开始体现了,而且越大越有优势。
论文里还提到了其他的优化思路,比如下面这篇文章的对直方图分级,不过我目前还没看懂怎么做,这个先挖个坑吧,等以后有机会再深挖:)。
A coarse-to-fine algorithm for fast median filtering of image data with a huge number of levels
还有在计算中值的时候其实是不需要每次都从头开始遍历直方图来计算中值的,下面这篇论文介绍了一个计算技巧可以减少计算中值的时间,有兴趣的读者可以看下: A fast two-dimensional median filtering algorithm
本文总阅读量次