【GiantPandaCV导语】本文记录了笔者最近的一些优化gemm的思路和实现，这些思路大多是公开的方案，例如来自how-to-optimize-gemm工程的一些优化手段，来自ncnn的一些优化手段等。最终，笔者目前实现的版本在armv7a上可以达到50%左右的硬件利用率（这个利用率的确还不高，笔者也是一步步学习和尝试，大佬轻喷），本文记录了这些思路以及核心实现方法。改好的行主序代码（x86+armv7a版本）可以直接访问https://github.com/BBuf/how-to-optimize-gemm获取。

1. 前言¶

首先，我想强调一点，判断一个算法的加速效果和速度一定要实测，尽量不要全信别人给出的benchmark数据，做任何事都需要静心一步步来。这篇文章是在基于how-to-optimize-gemm初探矩阵乘法优化的基础上做了更加精细的测试，另外参考了NCNN的 $1\times 1$ 卷积思路最后在单核A53上获得了45%的硬件利用率，如果将输入数据的Pack也提前做掉（类似于NC4HW4输入），则可以获得50%以上的硬件利用率。因此这篇文章将从上面介绍的各个优化点进行解析，并且此算法的最优版本已经集成到Msnhnet(https://github.com/msnh2012/Msnhnet)，读者也可以在里面看到。接下来我就直接介绍这一系列优化手段。

如果读者想具体看某一种优化的优化效果以及对应的代码实现，可以直接参考下面的结果表格（基于armv7a的结果），然后去https://github.com/BBuf/how-to-optimize-gemm/tree/master/armv7a/src下选择对应的源码文件查看即可：

文件名	优化方法	gFLOPs	峰值占比	线程数
MMult1.h	无任何优化	0.24gflops	2.1%	1
MMult2.h	一次计算4个元素	0.24gflops	2.1%	1
MMult_1x4_3.h	一次计算4个元素	0.24gflops	2.1%	1
MMult_1x4_4.h	一次计算4个元素	0.24gflops	2.1%	1
MMult_1x4_5.h	一次计算4个元素(将4个循环合并为1个)	0.25gflops	2.2%	1
MMult_1x4_7.h	一次计算4个元素(我们在寄存器中累加C的元素，并对a的元素使用寄存器),用指针来寻址B中的元素	0.98gflops	9.0%	1
MMult_1x4_8.h	在MMult_1x4_7的基础上循环展开四个（展开因子的相对任意选择）	1.1gflops	10%	1
MMult_4x4_3.h	一次计算C中的4x4小块	0.24gflops	2.1%	1
MMult_4x4_4.h	一次计算C中的4x4小块	0.24gflops	2.1%	1
MMult_4x4_5.h	一次计算C中的4x4小块,将16个循环合并一个	0.25gflops	2.2%	1
MMult_4x4_6.h	一次计算C中的4x4小块(我们在寄存器中累加C的元素，并对a的元素使用寄存器)	1.75gflops	16.0%	1
MMult_4x4_7.h	在MMult_4x4_6的基础上用指针来寻址B中的元素	1.75gflops	16.0%	1
MMult_4x4_8.h	使用更多的寄存器	1.75gflops	16.0%	1
MMult_4x4_10.h	NEON指令集优化	2.6gflops	23.8%	1
MMult_4x4_11.h	NEON指令集优化, 并且为了保持较小问题规模所获得的性能，我们分块矩阵C（以及相应的A和B）	2.6gflops	23.8%	1
MMult_4x4_13.h	NEON指令集优化, 对矩阵A和B进行Pack，这样就可以连续访问内存	2.6gflops	23.8%	1
conv1x1s1.h（version1）	一次计算多行，neon汇编优化	3.4gflops	31.0%	1
conv1x1s1.h（version2）	pack，kernel提前做，neon汇编优化	4.9gflops	45%	1
conv1x1s1.h（version3）	pack，kernel提前做，输入NC4HW4，neon汇编优化	5.5gflops	50.5%	1

为了大家看起来不累，这篇文章尽量不粘贴大段代码，我主要为大家介绍思路，代码可以到上面提供的源码仓库中查看。

2. 原始实现¶

这个非常简单，就是实现 $C=A*B$ ，其中 $C$ 的维度是 $[m, n]$ ， $A$ 的维度是 $[m,k]$ ， $B$ 的维度是 $[k, n]$ ，那么矩阵乘法的原始实现就是（注意，这里是行主序）：

#define A( i, j ) a[ (i)*lda + (j) ]
#define B( i, j ) b[ (i)*ldb + (j) ]
#define C( i, j ) c[ (i)*ldb + (j) ]
// gemm C = A * B + C
void MatrixMultiply(int m, int n, int k, float *a, int lda, float *b, int ldb, float *c, int ldc)
{
    for(int i = 0; i < m; i++){
        for (int j=0; j<n; j++ ){    
            for (int p=0; p<k; p++ ){      
                C(i, j) = C(i, j) + A(i, p) * B(p, j);
            }
        }
    }
}

这一个版本的gflops只有0.24g，硬件利用率只有1.4%，接下来我们就逐步进行优化。

3. 一次计算4个元素¶

这里一次计算4个元素的意思是一次计算 $C$ 矩阵也就是结果矩阵的 $4$ 个元素。在第二节的原始实现中，我们一次计算 $C$ 矩阵的一个元素，这个时候需要遍历A矩阵的一行和B矩阵的一列并做乘加运算。如果我们一次计算C矩阵的4个元素，那么我们可以每次遍历A矩阵的一行和B矩阵的四列，代码实现大概是这个样子：

void MY_MMult2( int m, int n, int k, float *a, int lda, 
                                    float *b, int ldb,
                                    float *c, int ldc ){
  int i, j;
  for ( j=0; j<n; j+=4 ){
    for ( i=0; i<m; i+=1 ){
      AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) );
      AddDot( k, &A( i,0 ), lda, &B( 0,j+1 ), &C( i,j+1 ) );
      AddDot( k, &A( i,0 ), lda, &B( 0,j+2 ), &C( i,j+2 ) );
      AddDot( k, &A( i,0 ), lda, &B( 0,j+3 ), &C( i,j+3 ) );
    }
  }
}

但是很遗憾，由于编译器开了O2，这种优化方法并不奏效，这个版本取得了和原始实现差不多的gflops。

4. 第一次还算有效的优化¶

第一次看起来比较有效的方法是引入寄存器变量。从计算机存储体系结构图(Figure3)可以看到寄存器变量离CPU是最近的，它的数据访问数据也是最快的，因此我们可以在求和的时候显示声明求和和被乘的变量为寄存器变量，这样在累加求和的时候访问速度会比原始版本更快一些，可以带来一些提升。

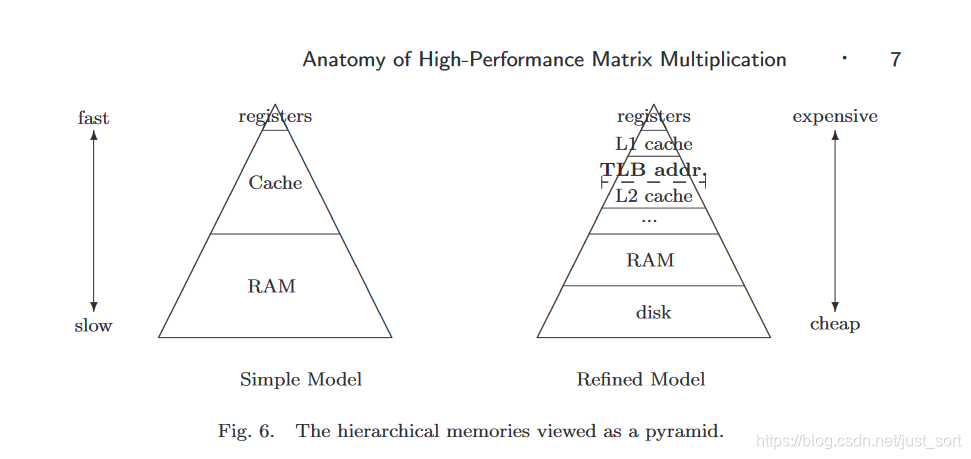
在这里插入图片描述

这部分的代码实现大致如下：

void AddDot1x4( int k, float *a, int lda,  float *b, int ldb, float *c, int ldc ){
  int p;
  register float c_00_reg, c_01_reg, c_02_reg, c_03_reg,   a_0p_reg;
  c_00_reg = 0.0; 
  c_01_reg = 0.0; 
  c_02_reg = 0.0; 
  c_03_reg = 0.0;
  for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );
    c_00_reg += a_0p_reg * B( p, 0 );     
    c_01_reg += a_0p_reg * B( p, 1 );     
    c_02_reg += a_0p_reg * B( p, 2 );     
    c_03_reg += a_0p_reg * B( p, 3 );     
  }
  C( 0, 0 ) += c_00_reg; 
  C( 0, 1 ) += c_01_reg; 
  C( 0, 2 ) += c_02_reg; 
  C( 0, 3 ) += c_03_reg;
}

这个版本的代码对应https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_1x4x6.h，取得了0.32gflops的成绩，在原始版本上有微弱提升。

5. 第一次提升较大的优化¶

在第一次优化的基础上，我们用指针来寻址A中的元素。因为这里实现的是行主序的矩阵乘法，因此每计算一个C中元素，对于A的任意一行的内存访问都是连续的，这样我们就可以用指针移位的方式代替数据访问的方式了。基于这个思路，我们可以将第4节的代码改写成下面的样子：

void AddDot1x4( int k, float *a, int lda,  float *b, int ldb, float *c, int ldc ){
  int p;
  register float c_00_reg,   c_01_reg,   c_02_reg,   c_03_reg,  b_0p_reg;
  float *ap0_pntr, *ap1_pntr, *ap2_pntr, *ap3_pntr;
  ap0_pntr = &A( 0, 0 );
  ap1_pntr = &A( 1, 0 );
  ap2_pntr = &A( 2, 0 );
  ap3_pntr = &A( 3, 0 );
  c_00_reg = 0.0; 
  c_01_reg = 0.0; 
  c_02_reg = 0.0; 
  c_03_reg = 0.0;
  for ( p=0; p<k; p++ ){
    b_0p_reg = B( p, 0 );
    c_00_reg += b_0p_reg * *ap0_pntr++;
    c_01_reg += b_0p_reg * *ap1_pntr++;
    c_02_reg += b_0p_reg * *ap2_pntr++;
    c_03_reg += b_0p_reg * *ap3_pntr++;
  }
  C( 0, 0 ) += c_00_reg; 
  C( 1, 0 ) += c_01_reg; 
  C( 2, 0 ) += c_02_reg; 
  C( 3, 0 ) += c_03_reg;
}

这样一个小的改动，我们获得了0.98gflops，硬件利用率来到了9%，这确实是一个提升较大的优化。这个版本的代码对应https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_1x4_7.h 。

6. 第三次优化，尝试更大的分块¶

在上面的几次优化中，我们一次计算C矩阵的一个元素或者C矩阵的4个元素，我们这一节将其扩展为一次计算C矩阵的16个元素，即 $4\times 4$ 分块方法。另外，我们使用寄存器变量累加C的元素，并对A的元素也使用寄存器变量。这部分代码实现也比较简单，可以在https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_4x4_6.h查看。经过 $4\times 4$ 分块后，我们获得了1.75gflops的结果，硬件利用率在16%左右。

接下来，参考第5节的思路，我们在/MMult_4x4_6的基础上用指针来寻址B中的元素，但因为 $4\times 4$ 分块本身对内存访问就有很大的改善，这个优化在这里作用不大。没有获得明显的gflops提升。这部分的代码实现对应https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_4x4_7.h

7. 第四次优化，Neon指令集优化¶

在计算C中的元素时，我们可以使用simd来进行优化，在Armv7a架构上即是将https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_4x4_10.h的核心实现部分用Neon指令集来进行优化，这里先使用Neon Instrics进行优化。

void AddDot4x4( int k, float *a, int lda,  float *b, int ldb, float *c, int ldc ){
  float  *a_0p_pntr, *a_1p_pntr, *a_2p_pntr, *a_3p_pntr;
  a_0p_pntr = &A(0, 0);
  a_1p_pntr = &A(1, 0);
  a_2p_pntr = &A(2, 0);
  a_3p_pntr = &A(3, 0);
  float32x4_t c_p0_sum = {0};
  float32x4_t c_p1_sum = {0};
  float32x4_t c_p2_sum = {0};
  float32x4_t c_p3_sum = {0};
  register float a_0p_reg, a_1p_reg, a_2p_reg, a_3p_reg;

  for (int p = 0; p < k; ++p) {
    float32x4_t b_reg = vld1q_f32(&B(p, 0));

    a_0p_reg = *a_0p_pntr++;
    a_1p_reg = *a_1p_pntr++;
    a_2p_reg = *a_2p_pntr++;
    a_3p_reg = *a_3p_pntr++;

    c_p0_sum = vmlaq_n_f32(c_p0_sum, b_reg, a_0p_reg);
    c_p1_sum = vmlaq_n_f32(c_p1_sum, b_reg, a_1p_reg);
    c_p2_sum = vmlaq_n_f32(c_p2_sum, b_reg, a_2p_reg);
    c_p3_sum = vmlaq_n_f32(c_p3_sum, b_reg, a_3p_reg);
  }

  float *c_pntr = 0;
  c_pntr = &C(0, 0);
  float32x4_t c_reg = vld1q_f32(c_pntr);
  c_reg = vaddq_f32(c_reg, c_p0_sum);
  vst1q_f32(c_pntr, c_reg);

  c_pntr = &C(1, 0);
  c_reg = vld1q_f32(c_pntr);
  c_reg = vaddq_f32(c_reg, c_p1_sum);
  vst1q_f32(c_pntr, c_reg);

  c_pntr = &C(2, 0);
  c_reg = vld1q_f32(c_pntr);
  c_reg = vaddq_f32(c_reg, c_p2_sum);
  vst1q_f32(c_pntr, c_reg);

  c_pntr = &C(3, 0);
  c_reg = vld1q_f32(c_pntr);
  c_reg = vaddq_f32(c_reg, c_p3_sum);
  vst1q_f32(c_pntr, c_reg);
}

之前和德澎在《AI移动端优化》专栏里面介绍过很多Neon指令集优化的例子，所以这里就不再详细上面的代码每行代表什么意思了，感兴趣的读者可以对比MMult_4x4_7.h的代码来理解。经过Neon Instrics优化之后，我们获得了2.6gflops的成绩，达到了23.8%的硬件利用率。

8. 第5次优化，数据Pack¶

在上面的优化中我们可以发现，在矩阵乘法的计算中，无论是行主序还是列主序，始终有一个矩阵的内存是没办法连续访问的。这也是为什么我们分块后gflops能获得较大提升的重要原因。因此，为了改善这个情况，我们执行数据Pack，将矩阵A和矩阵B的访问时的内存变成连续的。

理论上来说，这样做一定是有提升的，但是在Armv7a上实测发现gflops并没有提升（在x86上有4倍左右的gflops提升）。这里的原因猜测主要是Pack数据本身也需要时间，另外 $4\times 4$ 的分块已经较好的规避了内存不连续导致的访存时间消耗，当数据Pack的时间不可忽略时加速就非常少，而x86架构下的数据pack速度要优于armv7a架构（猜测，如果大佬有更好的解释，请联系我）。

因此，这里给我的启发是数据Pack尽量要在核心计算过程的外部完成。

9. 第6次优化，一次计算多行+Neon Assembly¶

首先我们知道，在CNN中 $1\times 1$ 卷积可以直接看成Kernel矩阵和输入特征图矩阵直接做矩阵乘法，我们可以把 $1\times 1$ 的卷积核看成矩阵乘法的矩阵A，它的维度是 $[outChannel，inChannel]$ 。然后再把输入特征图看成矩阵乘法的矩阵B，它的维度是 $[inChannel,inHeight*inWidth]$ ，这样矩阵C就是我们的 $1\times 1$ 卷积结果了，维度是 $[outChannel,inHeight*inWidth]$ ，因为 $1\times 1$ 卷积并且步长为 $1$ 的情况下输出特征图的长宽和输入特征图是完全一致的。

其中：

inChannel 表示卷积层的输入通道数
outChanenel 表示卷积层的输出通道数
inHeight 表示输入特征图的高度
inWidth 表示输入特征图的宽度

基于此，我参考了NCNN的 $1\times 1$ 卷积的第一版实现方法获得了本次优化的版本。完整实现在https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/convolution1x1s1.h#L10。主要思路就是一次计算 $4$ 行的输出，并且在每一行使用Neon指令集(Neon Assembly)进行优化，即在列方向再一次计算 $4$ 个元素。为了更好理解这个思路，下面我将这个函数Neon优化相关的部分去掉，留下了一个普通实现的代码如下，可以帮助读者快速理解这个算法。

void conv1x1s1(float *const &src, const int &inWidth, const int &inHeight,  const int &inChannel, float *const &kernel,
                                 float* &dest, const int &outWidth, const int &outHeight, const int &outChannel){
        int ccOutChannel = outChannel >> 2;
        int ccRemainOutChannel = ccOutChannel << 2;
        const int in_size = inWidth * inHeight;
        const int out_size = outWidth * outHeight;
        for(int cc = 0; cc < ccOutChannel; cc++){
            int c = cc << 2;

            float *dest0 = dest + c * out_size;
            float *dest1 = dest + (c + 1) * out_size;
            float *dest2 = dest + (c + 2) * out_size;
            float *dest3 = dest + (c + 3) * out_size;

            int q = 0;

            for(q = 0; q + 3 < inChannel; q += 4){
                float *destptr0 = dest0;
                float *destptr1 = dest1;
                float *destptr2 = dest2;
                float *destptr3 = dest3;

                const float *src0 = src + q * in_size;
                const float *src1 = src + (q + 1) * in_size;
                const float *src2 = src + (q + 2) * in_size;
                const float *src3 = src + (q + 3) * in_size;

                const float *r0 = src0;
                const float *r1 = src1;
                const float *r2 = src2;
                const float *r3 = src3;

                const float *kernel0 = kernel + c * inChannel + q;
                const float *kernel1 = kernel + (c + 1) * inChannel + q;
                const float *kernel2 = kernel + (c + 2) * inChannel + q;
                const float *kernel3 = kernel + (c + 3) * inChannel + q;
                int remain = out_size;
                for(; remain > 0;  remain--){
                    float sum0 = *r0 * kernel0[0] + *r1 * kernel0[1] + *r2 * kernel0[2] + *r3 * kernel0[3];
                    float sum1 = *r0 * kernel1[0] + *r1 * kernel1[1] + *r2 * kernel1[2] + *r3 * kernel1[3];
                    float sum2 = *r0 * kernel2[0] + *r1 * kernel2[1] + *r2 * kernel2[2] + *r3 * kernel2[3];
                    float sum3 = *r0 * kernel3[0] + *r1 * kernel3[1] + *r2 * kernel3[2] + *r3 * kernel3[3];

                    *destptr0 += sum0;
                    *destptr1 += sum1;
                    *destptr2 += sum2;
                    *destptr3 += sum3;

                    r0++;
                    r1++;
                    r2++;
                    r3++;
                    destptr0++;
                    destptr1++;
                    destptr2++;
                    destptr3++;
                }
            }

            for(; q < inChannel; q++){
                float *destptr0 = dest0;
                float *destptr1 = dest1;
                float *destptr2 = dest2;
                float *destptr3 = dest3;

                const float *src0 = src + q * in_size;
                const float *kernel0 = kernel + c * inChannel + q;
                const float *kernel1 = kernel + (c + 1) * inChannel + q;
                const float *kernel2 = kernel + (c + 2) * inChannel + q;
                const float *kernel3 = kernel + (c + 3) * inChannel + q;
                const float *r0 = src0;
                int remain = out_size;
                for(; remain > 0; remain--){
                    float sum0 = *r0 * kernel0[0];
                    float sum1 = *r0 * kernel1[0];
                    float sum2 = *r0 * kernel2[0];
                    float sum3 = *r0 * kernel3[0];

                    *destptr0 += sum0;
                    *destptr1 += sum1;
                    *destptr2 += sum2;
                    *destptr3 += sum3;

                    r0++;
                    destptr0++;
                    destptr1++;
                    destptr2++;
                    destptr3++;
                }

            }
        }
        for(int cc = ccRemainOutChannel; cc < outChannel; cc++){
            float *dest0 = dest + cc * out_size;
            int q = 0;
            for(; q + 3 < inChannel; q += 4){
                float *destptr0 = dest0;
                const float *src0 = src + q * in_size;
                const float *src1 = src + (q + 1) * in_size;
                const float *src2 = src + (q + 2) * in_size;
                const float *src3 = src + (q + 3) * in_size;
                const float *r0 = src0;
                const float *r1 = src1;
                const float *r2 = src2;
                const float *r3 = src3;
                const float *kernel0 = kernel + cc * inChannel + q;
                int remain = out_size;
                for(; remain > 0; remain--){
                    float sum0 = *r0 * kernel0[0] + *r1 * kernel0[1] + *r2 * kernel0[2] + *r3 * kernel0[3];

                    *destptr0 += sum0;

                    r0++;
                    r1++;
                    r2++;
                    r3++;
                    destptr0++;
                }

            }

            for(; q < inChannel; q++){
                float *destptr0 = dest0;
                const float *src0 = src + q * in_size;
                const float *kernel0 = kernel + cc * inChannel + q;
                const float *r0 = src0;
                int remain = out_size;
                for(; remain > 0; remain--){
                    float sum0 = *r0 * kernel0[0];

                    *destptr0 += sum0;

                    r0++;
                    destptr0++;
                }

            }
        }
}

将上面的代码进行Neon Assembly优化然后进行测试，我们获得了3.4gflops的成绩，硬件利用率达到了31%，是当前的最好成绩。

10. 第7次优化，数据Pack显威力¶

由于第6次优化的实现并未考虑到数据Pack的原因，所以访存是比较差的，这里可以使用Pack策略对其进行优化。这个思路我已经在详解Im2Col+Pack+Sgemm策略更好的优化卷积运算用各种图例讲得还算清楚了，另外MsnhNet的作者之前也做过一篇关于NC4HW4的图解图解神秘的NC4HW4，所以这里不再重复数据Pack的好处以及我这里具体是如何做数据Pack的，感兴趣的请直接移步源码。

将卷积核进行数据Pack（只用做一次，不会影响gflops），然后对输入数据进行Pack（注意Version2是每次计算过程都要做一次输入数据的Pack，所以数据输入Pack的时间也会影响gflops），然后进行计算。这部分的代码实现在https://github.com/msnh2012/Msnhnet/blob/master/src/layers/arm/MsnhConvolution1x1.cpp#L598。

对这个版本进行测试，我们获得了4.9gflops的成绩，达到了硬件利用率的49.5%。

另外，我们考虑一下如果将输入的排布变成NC4HW4的方式，那么输入数据的Pack时间也可以省掉，通过这样操作，我获得了5.5gflops的结果，达到了硬件利用率的50.5%。代码实现在：https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/convolution1x1s1.h 。

11. 总结¶

这篇文章主要是记录一下这两周对gemm算法优化的一些研究，然后我是如何一步步将矩阵乘法的硬件利用率做到了50%。当然，这个硬件利用率并不高，我也会持续学习和优化，欢迎大家提出建议和关注我们公众号GiantPandaCV，您的关注是我最大的鼓励。

12. 参考链接¶

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。

公众号QQ交流群

本文总阅读量次