EasyQuant 后量化算法论文解读
本文首发于 GiantPandaCV:EasyQuant 论文解读
本文的主要内容是解读 EasyQuant: Post-training Quantization via Scale Optimization¶
这篇由格灵深瞳出品的文章。
论文地址: https://arxiv.org/pdf/2006.16669.pdf
论文代码: https://github.com/deepglint/EasyQuant
前言:¶
这篇文章提出的后训练量化算法的思路是,引入相似性作为目标函数,通过交替搜索权值和激活的量化因子(scale)来最大化量化前后激活值的
相似性,来找到权值和激活值的最优量化因子。
而实际端上推理阶段则采用权值和激活 int7 量化,中间 int16 累加器累加多次的方式,使得推理速度优于权值和激活 int8 量化,中间 int16 累加器只累加两次的方式,同时还可以比较好的保持量化后算法的精度。
之前一些的量化方法算法的不足:¶
TensorRT的后量化算法与谷歌提出的训练量化等方法,有个共同点是对于权值的量化,都是直接取绝对值最大作为量化因子,也就是 。
每层激活量化因子的计算方式:
TensorRT采用的方法是过两遍校验集,第一遍统计该层激活绝对值的最大值 ,第二遍先把区间
分为2048份然后统计直方图,统计完成之后搜索直方图[128,2048]的区间,通过计算KL散度的方式来确定最佳阈值从而得到量化因子,更详细的内容可以看参考资料
[4,5]。
而谷歌提出的训练量化方法则是,在训练中采用 (exponential moving average) 的方式统计量化因子
[6],具体公式是
其中 表示当前batch的激活值,
一般取0.95,训练完成之后量化因子可以通过公式
获得。
该论文则指出这些方法主要的不足之处在于
-
只优化激活的量化因子而权值直接取最大值做量化的话其实会造成误差积累的问题,所以权值的量化因子也要优化;
-
在优化量化因子的时候,并没有考虑卷积层原始浮点输出与量化版本实现输出的分布的相似性。
论文算法解读¶
量化的定义¶
首先来看下量化的一般公式:
其中表示需要量化的张量,
表示量化因子,
表示量化之后的张量,
操作论文里表示向上取整的意思,
表示elementwise点乘操作,而
则表示饱和操作,比如量化到 int8,就是把量化后值限定在 [-128,127] 之间,超出的值取边界值。
然后论文用 ,表示一个经过量化的L层网络,其中
,
和
分别表示第l层的激活值(根据给定的一批校验集获得),权值和量化因子,都是float32类型。
包含两部分,第l层的激活量化因子
和权值量化因子
,其中权值的量化可以分通道(每个通道分别对应一个量化因子)或者不分通道(所有通道共用一个量化因子)。
接着定义 表示原始预训练模型第l层的激活值(float32),
表示量化权值(int8)和输入激活(int8)得到的第l层量化输出激活(int32)再反量化的结果(float32),公式如下:
优化目标¶
量化推理的流程图¶
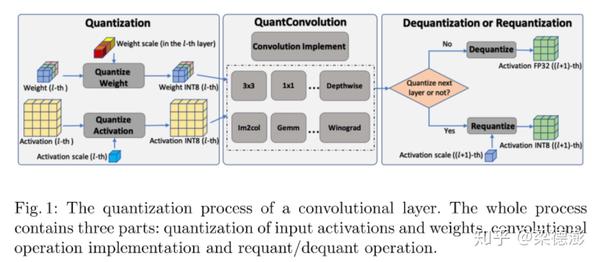
https://arxiv.org/pdf/2006.16669.pdf
首先看下论文里的这张图片,展示了第l层卷积层量化推理的流程图。
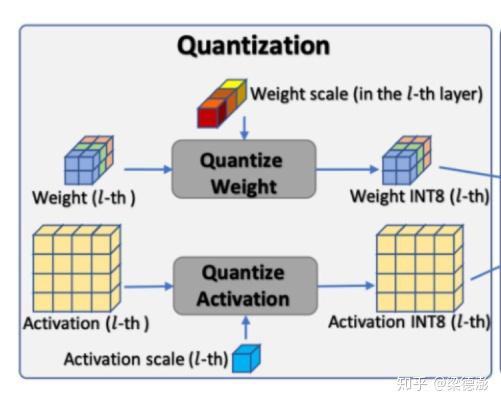
https://arxiv.org/pdf/2006.16669.pdf
首先看最左边的方框,权值和激活从float32量化到int8,权值因为可以分通道量化,所以可以看到权值的量化因子是分了3种不同颜色的立方体分别对应了权值3个不同颜色的通道。
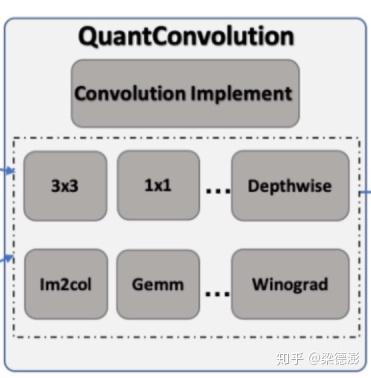
https://arxiv.org/pdf/2006.16669.pdf
然后中间的方框,表示推理阶段量化版本卷积的实现,可以看到有根据kernel设置分别优化,还有具体实现上用 im2col+gemm 或者 Winograd 优化实现等等
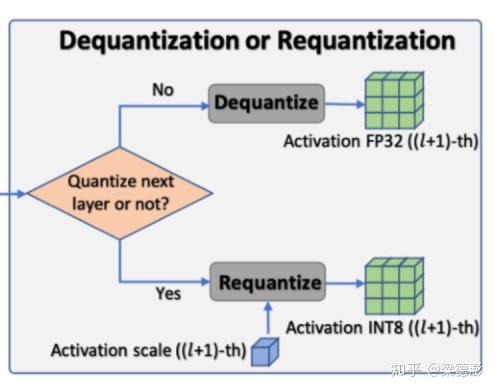
https://arxiv.org/pdf/2006.16669.pdf
最后看最右边的方框,表示得到卷积层输出量化激活结果之后,如果下一层不是量化计算层,则直接除以权值和输入激活的量化因子,得到反量化的输出(Dequantize)。如果下一层也是量化层,则除了除以权值和输入激活的量化因子还需要再乘以下一层的输入量化因子得到量化后的下一层的输入(Requantize)。
优化单层量化因子¶
接着看下论文提出的优化目标函数:
最大化第l层原始浮点激活输出与量化实现得到反量化输出的
相似性,也就是
距离越大越好。 然后优化过程分为两步,首先固定激活的量化因子
,通过最大化
相似性优化权值量化因子
。接着固定权值量化因子
优化激活量化因子
。然后,交替优化一直到
的值收敛或者超出预定的时间。
然后 用权值最大值来做初始化的,而
根据官方release的代码用的是TensorRT的方法来初始化的,有兴趣的可以去看下:
https://github.com/deepglint/EasyQuant/blob/f2f2e6cf38/tools/caffe_quanttable_e2e.py#L428
然后对于优化目标函数时,量化因子的搜索设置,论文是把区间
分成n份,然后搜索最佳量化因子,在实验中设置
,
还有
:

但是我去看了官方的代码,对于权值的优化,设置的搜索区间是
[1, Sl^w] 和 :
https://github.com/deepglint/EasyQuant/blob/f2f2e6cf38/tools/scale_fine_tuning.py#L351
然后对于激活的量化因子的优化,设置的搜索区间是 [0.8*Sl^a, Sl^a]和
https://github.com/deepglint/EasyQuant/blob/f2f2e6cf38/tools/scale_fine_tuning.py#L423
和论文中的设置太一样,我看issue上也有人提出了这个疑问:

https://github.com/deepglint/EasyQuant/issues/3
作者回复说推荐按照论文里面的设置,大家如果自己做实验的时候可以结合论文和官方代码。
优化整个网络¶
然后看下对于整个网络的优化算法流程图:

https://arxiv.org/pdf/2006.16669.pdf
可以看到是交替优化权值和激活,但是这里我看是先固定激活的量化因子,然后优化每一层的权值因子,然后固定每一层的权值因子,再优化逐层优化激活因子,同时在优化激活因子的时候,是每一层激活优化完成之后,更新下一层的量化计算激活值
,更具体的细节可以参考官方代码。
端上部署 int7 加速¶
 https://arxiv.org/pdf/2006.16669.pdf
https://arxiv.org/pdf/2006.16669.pdf
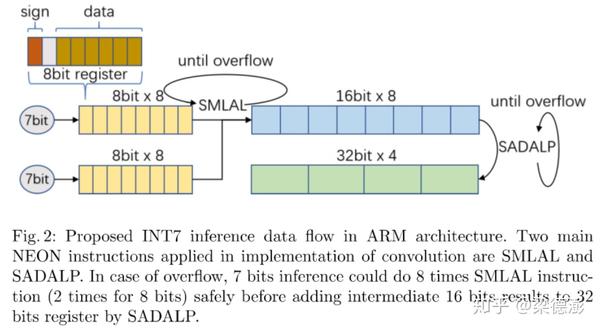
上面是论文给出的Arm 端int7CPU推理加速计算流程图。
其中论文中提到了, neon 指令表示向量乘加长指令,把两个8bit数据相乘产生16bit结果,然后累加到16bit中间结果上,
neon指令,则表示把两个16bit结果相加产生32bit然后累加到32bit累加结果上。
这两个指令我以前是没用过,如果对于具体实现上用的哪些指令感兴趣的话,可以看下 ncnn-int8-e2e :
https://github.com/deepglint/eq-ncnn
是基于ncnn int8社区版本低比特(小于8bit)量化魔改版。
然后看到端上推理流程图最上角,因为用的是量化到int7 [-63,63],所以8bit除去符号位,还有1bit剩余。这样就可以比量化到int8多累加几次到中间16bit结果上,

https://arxiv.org/pdf/2006.16669.pdf
比如论文中提到 int8 只能做两次 指令,然后中间16bit结果就要累加到32bit上,因为 8bit
取值区间是 [-2^7, 2^7-1],所以两个8bit相乘之后取值区间是
,然后累加两次就到了
,所以最多只能累加两次,其实第二次也已经有溢出风险了,因为如果相邻两次乘法结果都恰好是
,那就会超了
int16正数可表示的最大值。所以谷歌那篇训练量化的论文提到了,权值可以考虑量化到 [-127,127],就是这么个道理:

https://arxiv.org/pdf/1712.05877.pdf
这样子一次乘法计算结果永远是小于,那么就可以安全的累加两次相邻的乘法计算结果到int16中间结果上,然后再累加到32bit。
然后对于 7bit 取值区间是 [-2^6-1, 2^6-1],所以两个7bit相乘之后取值区间是
,所以可以安全的累加8次到int16中间结果上,然后再累加到32bit。所以相对于int8,int7可以有更好的加速效果。
实验结果分析:¶
实验设置¶
论文对比了 TensorRT 的方法,对于TensorRT 量化参数的计算,采用了1000个样本,而对于本论文的方法则是采用了50个样本来搜索量化参数,感觉还是挺惊人的,只用50个样本就能超过TensorRT的方法。
精度对比¶
https://arxiv.org/pdf/2006.16669.pdf
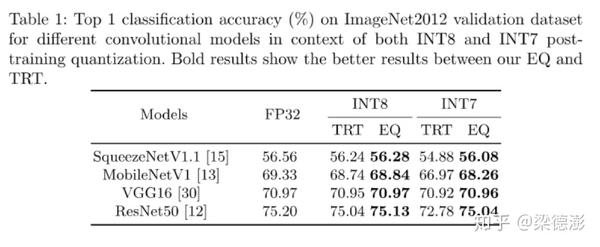
在imagenet2012验证集上的结果,可以看到不管是量化到int8还是int7,EasyQuant的精度都超过TensorRT,而且很接近浮点的结果。

https://arxiv.org/pdf/2006.16669.pdf
然后从物体检测和人脸任务上来看,EasyQuant基本也是超过TensorRT的。
https://arxiv.org/pdf/2006.16669.pdf
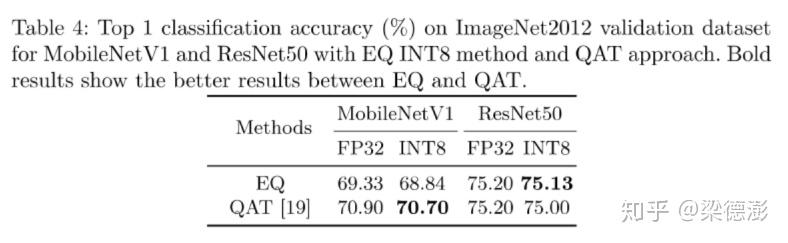
实验还对比了 EasyQuant和 训练量化QAT(Quantize Aware Training),可以按到在ResNet50上结果还是不错的,稍微超过QAT。
加速对比¶

https://arxiv.org/pdf/2006.16669.pdf
然后来看下实际端上推理时候 int8 和 int7 的推理速度对比,可以看到不管是单线程还是多线程,int7 推理的延迟都要少于 int8,有20%~30%的效率提升的效果,还是挺可观的。
更低bit实验结果¶
https://arxiv.org/pdf/2006.16669.pdf
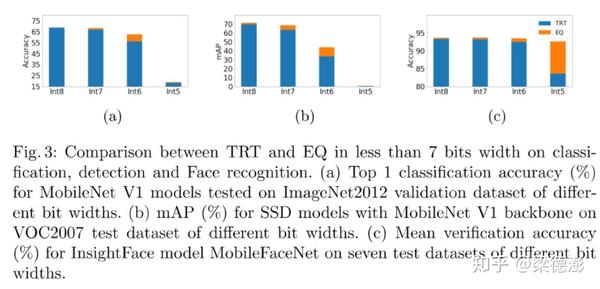
论文中还做了更低 bit 的对比实验,从 int8 到 int5,可以看到在不同任务上,EasyQuant 方法大多是优于 TensorRT 的方法的,而且让人惊讶的是图©,int5 EasyQuant 的精度基本和 int8 相当,没有降多少,这个确实很厉害。
总结¶
这篇论文提出了一个在低于8bit下精度还能保持比较好的后量化算法,思想相对TensorRT的方法来说更加容易理解,而且实现上也更加的容易,实际端侧推理加速效果也不错。
参考资料:¶
- [1] https://zhuanlan.zhihu.com/p/151383244
- [2] https://zhuanlan.zhihu.com/p/151292945
- [3] https://www.yuque.com/yahei/hey-yahei/quantization.mxnet2
- [4] http://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf
- [5] https://arleyzhang.github.io/articles/923e2c40/
- [6] https://zhuanlan.zhihu.com/p/65468307
欢迎关注GiantPandaCV公众号, 我们会坚持原创和分享我们学习到的新鲜知识。
有对文章相关的问题或者想要加入交流群,欢迎添加本人微信(添加时请说明来意):

本文总阅读量次