本文首发于GiantPandaCV公众号。

1. 前言¶

这篇文章首先详细介绍了DoreFaNet任意比特量化网络的原理，然后提供了DoreFaNet的Pytorch代码实现解析，并给出将DoreFa-Net应用到YOLOV3模型上之后的精度测试结果。论文原文：https://arxiv.org/pdf/1606.06160.pdf 。

2. DoreFa-Net¶

和前面我们讲过的BNN和TWN相比，DoreFa-Net并没有针对卷积层输出的每一个卷积核计算比例因子，而是直接对卷积层的整体输出计算一个比例因子，这样就可以简化反向传播时候的运算，因为在DoreFa-Net中反向传播也要量化。

首先我们介绍一下DoreFa-Net中的比特卷积核，然后详细说明如何使用低比特的方法量化权值，激活值以及梯度。

2.1 比特卷积核¶

我们知道，BNN中的点积可以用下面的公式表示：

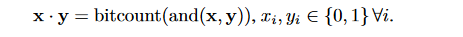
在这里插入图片描述

上面的式子同样也可以用在计算低位宽定点整数之间的乘加运算。假设 $x$ 是一个 $M$ 位定点整数序列集合， $x=\sum_{m=0}^{M-1}c_m(x)$ ， $y$ 是一个 $K$ 位定点整数序列集合， $y=\sum_{k=0}^{K-1}c_k(y)$ ，这里的 $(c_m(x))_{m=0}^{M-1}$ 和 $(c_k(y))_{k=0}^{K-1}$ 都是位向量， $x$ 和 $y$ 的点积可以由位运算来计算：

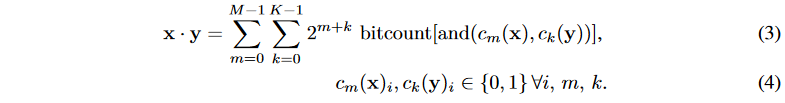在这里插入图片描述在上面的等式中，计算复杂度为 $M*K$ ，和位宽成正比。

2.2 直通估计器¶

然后为了规避0梯度的问题，使用了直通估计（STE）。

使用直通估计器(STRAIGHT-THROUGHESTIMATOR,STE)的原因可以用一个例子加以说明，假如网络有一个ReLU激活函数，并且网络被初始时即存在一套权重。这些ReLU的输入可以是负数，这会导致ReLU的输出为0。对于这些权重，ReLU的导数将会在反向传播过程中为0，这意味着该网络无法从这些导数学习到任何东西，权重也无法得到更新。针对这一点，直通估计器将输入的梯度设置为一个等于其输出梯度的阈值函数，而不管该阈值函数本身的实际导数如何。

一个简单的例子是在伯努利分布采样中定义的STE为：

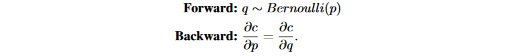
在这里插入图片描述

在这里， $c$ 是目标函数，由于从伯努利分布中采样是一个不可微分的过程， $\frac{\partial c}{\partial q}$ 没有定义，因此反向传播中的梯度不能由链式法则直接算出 $\frac{\partial c}{\partial p}$ ，然而由于 $p$ 和 $q$ 的期望相同，我们可以使用定义好的梯度 $\frac{\partial c}{\partial q}$ 对 $\frac{\partial c}{\partial p}$ 做近似，并且构建了一个如上所示的STE，因此STE实际上给出了一个对 $\frac{\partial c}{\partial p}$ 的定义。在本文的工作中广泛使用的STE是量化器---将一个真实的浮点数输入 $r_i\in [0,1]$ 量化未 $k$ 位输出 $r_o\in [0,1]$ ，定义的STE如下：

STE

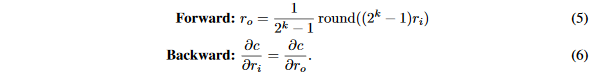
我们可以看到，直通估计器STE的输出 $q$ 是一个由 $k$ 位表示的真实数，由于 $r_o$ 是一个 $k$ 位定点整数，卷积计算可以由等式(3)高效执行，后面跟着正确的缩放即可。

2.3 权重的低比特量化¶

在之前的工作中，STE被用来做二值化权重，比如在BNN中，权重被下面的STE二值化：

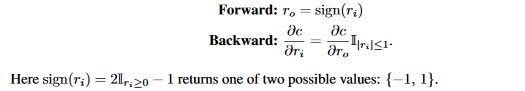
BNN STE

在XNOR-Net中，权重按照下面的STE二值化，不同之处在于权重在二值化之后进行了缩放：

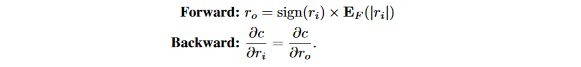
XORNet STE

在XOR-Net中，缩放因子 $E_{F}(|r_i|)$ 是对应卷积核的权重绝对值均值。理由是引入这个缩放因子将会增加权重表达范围，同时仍然可以在前向传播卷积时做位运算。因此，在本文的实验中，使用一个常量缩放因子来替代通道级缩放。在这篇论文中，对于所有的二值化权重使用同一个缩放因子：

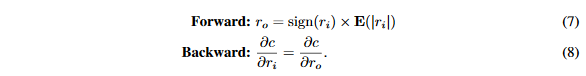
DoReFa-Net STE

当 $k>1$ 时，论文使用 $k$ 位表达的权重，然后将STE $f_{w}^k$ 应用在权重上：

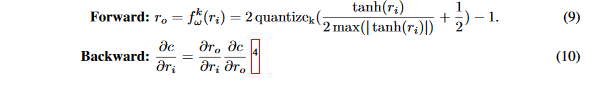
在这里插入图片描述

在量化到 $k$ 位之前，论文先使用tanh将权重限制在[-1,1]之间。通过 $\frac{tanh(r_i)}{2max(|tanh(r_i)|)}+1/2$ 将数值约束在[0,1]之间，最大值是相对于整个层的权重而言的。然后通过：

$quantize_k=\frac{1}{2^k-1}round((2^k-1)r_i)$

将浮点数转换位 $k$ 位定点数，范围在 $[0,1]$ ，最后通过映射变换将 $r_o$ 约束到 $[-1,1]$ 。

需要注意的是，当k=1时，等式9不同于等式7，它提供了一个不同的二值化权重的方法，然而，论文发现在实验中这种区别不重要。

2.4 梯度的低比特量化¶

本文已经证明了确定性量化可以产生低位宽的权重和激活值。然后，为了将梯度也量化到低位宽，保持梯度的无界是非常重要的，同时梯度应该比激活值的范围更广。回顾等式（9），我们通过可微分的非线性激活函数将激活值约束到了 $[0,1]$ ，然而，这种构造不存在渐变，因此我们对梯度设计了如下的 $k$ 位量化方式：

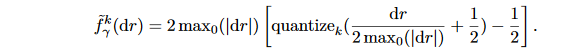
在这里插入图片描述

这里的 $dr=\frac{\partial c}{\partial r}$ 是一些层的输出 $r$ 对损失函数 $c$ 的导数，最大值是对梯度张量所有维度（除了 $batch size$ ）的统计，然后在梯度上用来放缩将结果映射到 $[0,1]$ 之间，然后在量化之后又放缩回去。

然后，为了进一步补偿梯度量化引入的潜在偏差，我们引入了额外的函数 $N(k)=\frac{\sigma}{2^k-1}$ ，这里

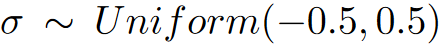
$\sigma$

因此，噪声可能具有和量化误差相同的幅值。论文发现，人工噪声对性能的影响很大，最后，论文做 $k$ 位梯度量化的表达式如下：

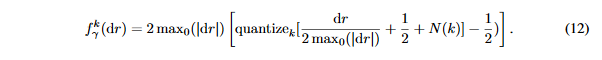
在这里插入图片描述

梯度的量化仅仅在反向传播时完成，因此每一个卷积层的输出上的STE是：

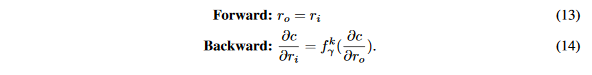
在这里插入图片描述

2.5 DoReFa-Net训练算法¶

论文给出了DoReFa-Net的训练算法，如Algorithm1所示。假设网络具有前馈线性拓扑，像BN层、池化层这样的细节在这里不详细展开。要注意的是，所有昂贵的操作如forward，backward_input，backward_weight（无论是卷积层还是全连接层），都是在低Bit上做的。通过构造，在这些低位宽数字和定点整数之间总是存在仿射映射的，因此，所有昂贵的操作都可以通过定点整数之间的点积等式（3）来加速。

Algorithm1

2.6 小结¶

最终，我们获得了DoreFa-Net的算法，这里对第一层和最后一层不做量化，因为输入层对图像任务来说通常是8bit的数据，做低比特量化会对精度造成很大的影响，输出层一般是一些One-Hot向量，因此输出层也要保持原样。DoreFa-Net分别对SVHN和ImageNet做了实验，其准确率明显高于二值化网络和三值化网络。

3. 代码实战¶

仍然以666DZY666博主分享的Pytorch实现为例子来介绍一下DoreFa-Net的代码实现，代码地址为：

https://github.com/666DZY666/model-compression

首先我们看一下使用DoreFa-Net算法搭建的网络，代码目录为del-compression/blob/master/quantization/WqAq/dorefa/models/nin.py：

# 注意这个代码中对卷积层和全连接层实现了DoreFa-Net的量化方法
import torch
import torch.nn as nn
import torch.nn.functional as F
from .util_wqaq import Conv2d_Q

class DorefaConv2d(nn.Module):
    def __init__(self, input_channels, output_channels,
            kernel_size=-1, stride=-1, padding=-1, groups=1, last_relu=0, abits=8, wbits=8, first_layer=0):
        super(DorefaConv2d, self).__init__()
        self.last_relu = last_relu
        self.first_layer = first_layer

        self.q_conv = Conv2d_Q(input_channels, output_channels,
                    kernel_size=kernel_size, stride=stride, padding=padding, groups=groups, a_bits=abits, w_bits=wbits, first_layer=first_layer)
        # BN和激活都保留了常规方式
        self.bn = nn.BatchNorm2d(output_channels)
        self.relu = nn.ReLU(inplace=True)

    def forward(self, x):
        # 第一个卷积层后面不接relu激活函数
        if not self.first_layer:
            x = self.relu(x)
        x = self.q_conv(x)
        x = self.bn(x)
        # 最后一层卷积层后要使用relu激活函数
        if self.last_relu:
            x = self.relu(x)
        return x

class Net(nn.Module):
    def __init__(self, cfg = None, abits=8, wbits=8):
        super(Net, self).__init__()
        if cfg is None:
            # 网络层通道数
            cfg = [192, 160, 96, 192, 192, 192, 192, 192]

        # model - A/W全量化(除输入、输出外)   
        self.dorefa = nn.Sequential(
                DorefaConv2d(3, cfg[0], kernel_size=5, stride=1, padding=2, abits=abits, wbits=wbits, first_layer=1),
                DorefaConv2d(cfg[0], cfg[1], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits),
                DorefaConv2d(cfg[1], cfg[2], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits),
                nn.MaxPool2d(kernel_size=3, stride=2, padding=1),

                DorefaConv2d(cfg[2], cfg[3], kernel_size=5, stride=1, padding=2, abits=abits, wbits=wbits),
                DorefaConv2d(cfg[3], cfg[4], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits),
                DorefaConv2d(cfg[4], cfg[5], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits),
                nn.MaxPool2d(kernel_size=3, stride=2, padding=1),

                DorefaConv2d(cfg[5], cfg[6], kernel_size=3, stride=1, padding=1, abits=abits, wbits=wbits),
                DorefaConv2d(cfg[6], cfg[7], kernel_size=1, stride=1, padding=0, abits=abits, wbits=wbits),
                DorefaConv2d(cfg[7], 10, kernel_size=1, stride=1, padding=0, last_relu=1, abits=abits, wbits=wbits),
                nn.AvgPool2d(kernel_size=8, stride=1, padding=0),
                )

    def forward(self, x):
        x = self.dorefa(x)
        x = x.view(x.size(0), -1)
        return x

可以看到这个代码的核心是调用了DorefaConv2d这个DoreFa量化卷积层，这个实现在https://github.com/666DZY666/model-compression/blob/master/quantization/WqAq/dorefa/models/util_wqaq.py中，即：

# ********************* 量化卷积（同时量化A/W，并做卷积） ***********************
class Conv2d_Q(nn.Conv2d):
  def __init__(
        self,
        in_channels,
        out_channels,
        kernel_size,
        stride=1,
        padding=0,
        dilation=1,
        groups=1,
        bias=True,
        a_bits=8,
        w_bits=8,
        first_layer=0
      ):
        super().__init__(
            in_channels=in_channels,
            out_channels=out_channels,
            kernel_size=kernel_size,
            stride=stride,
            padding=padding,
            dilation=dilation,
            groups=groups,
            bias=bias
        )
        # 实例化调用A和W量化器
        self.activation_quantizer = activation_quantize(a_bits=a_bits)
        self.weight_quantizer = weight_quantize(w_bits=w_bits)    
        self.first_layer = first_layer

  def forward(self, input):
    # 量化A和W
    if not self.first_layer:
      input = self.activation_quantizer(input)
    q_input = input
    q_weight = self.weight_quantizer(self.weight) 
    # 量化卷积
    output = F.conv2d(
            input=q_input,
            weight=q_weight,
            bias=self.bias,
            stride=self.stride,
            padding=self.padding,
            dilation=self.dilation,
            groups=self.groups
        )
    return output

对于权重的量化代码实现如下，对应了公式9和公式10：

# ********************* W(模型参数)量化 ***********************
class weight_quantize(nn.Module):
  def __init__(self, w_bits):
    super().__init__()
    self.w_bits = w_bits

  def round(self, input):
    output = Round.apply(input)
    return output

  def forward(self, input):
    if self.w_bits == 32:
      output = input
    elif self.w_bits == 1:
      print('！Binary quantization is not supported ！')
      assert self.w_bits != 1                      
    else:
      # 按照公式9和10计算
      output = torch.tanh(input)
      output = output / 2 / torch.max(torch.abs(output)) + 0.5  #归一化-[0,1]
      scale = float(2 ** self.w_bits - 1)
      output = output * scale
      output = self.round(output)
      output = output / scale
      output = 2 * output - 1
    return output

其中round函数的实现如下，可以看到继承了torch.autograd.Function，使得这个round操作可以反向传播：

class Round(Function):

    @staticmethod
    def forward(self, input):
        output = torch.round(input)
        return output

    @staticmethod
    def backward(self, grad_output):
        grad_input = grad_output.clone()
        return grad_input

然后对于激活值的量化，论文中的介绍如下图所示：

DoreFa-Net对激活值的量化

代码实现如下：

# ********************* A(特征)量化 ***********************
class activation_quantize(nn.Module):
  def __init__(self, a_bits):
    super().__init__()
    self.a_bits = a_bits

  def round(self, input):
    output = Round.apply(input)
    return output

  def forward(self, input):
    if self.a_bits == 32:
      output = input
    elif self.a_bits == 1:
      print('！Binary quantization is not supported ！')
      assert self.a_bits != 1
    else:
      output = torch.clamp(input * 0.1, 0, 1)  # 特征A截断前先进行缩放（* 0.1），以减小截断误差
      scale = float(2 ** self.a_bits - 1)
      output = output * scale
      output = self.round(output)
      output = output / scale
    return output

注意一下这里有个Trick，即特征A截断前先进行缩放（* 0.1），以减小截断误差。

代码中还实现了全连接层量化：

# ********************* 量化全连接（同时量化A/W，并做全连接） ***********************
class Linear_Q(nn.Linear):
  def __init__(self, in_features, out_features, bias=True, a_bits=2, w_bits=2):
    super().__init__(in_features=in_features, out_features=out_features, bias=bias)
    self.activation_quantizer = activation_quantize(a_bits=a_bits)
    self.weight_quantizer = weight_quantize(w_bits=w_bits) 

  def forward(self, input):
    # 量化A和W
    q_input = self.activation_quantizer(input)
    q_weight = self.weight_quantizer(self.weight) 
    # 量化全连接
    output = F.linear(input=q_input, weight=q_weight, bias=self.bias)
    return output

4. 将DoreFa-Net应用到YOLOV3上¶

上次介绍的YOLOV3剪枝方法汇总文章中还剩下一个量化方法当时没有提到，实际上它的量化方法就是DoreFa-Net的量化方法，所以我们来看一下量化效果：

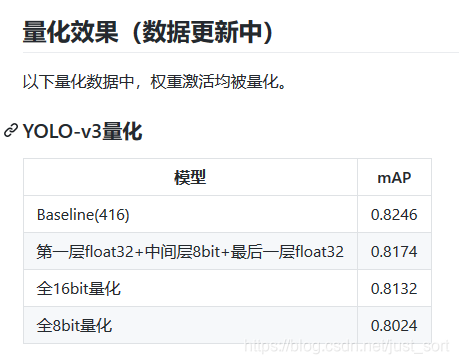
YOLOV3使用DoreFa-Net的量化实验结果

但是需要注意的是，在框架下量化训练过程都还是在float32精度下的表达，只是尺度scale到量化的尺度上了，能够验证量化的有效性。但如果要实际部署，可以看下我们发布的深度学习量化技术科普，并且后续我也会更新实际工程中的做量化加速的一些分享。

5. 总结¶

这篇文章，从算法原理和代码实现方面剖析了DoreFa-Net，并验证了DoreFaNet的有效性，并且可以看到通过这种方法INT8的掉点情况完全可以接受。

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。

公众号QQ交流群

本文总阅读量次