基于一阶泰勒展开式的结构化剪枝

【GiantPandaCV导语】文章是Nvidia在2017年ICLR发表的，核心思路是将结构化通道剪枝判别依据视为一个优化问题，即最小化剪枝后前后的代价函数之间的差。把优化问题基于一阶泰勒展开式近似，得到通道重要性的判据只需要考虑激活函数与对应的梯度的乘积，再求其均值。为了跨层的公平性加上重要性归一化，以及加入Flops正则化。

0.引言¶

文章是NVIDIA在2017 ICLR上面发表的，《Pruning convolution Neural Network for resource efficient inference》。其核心也是将结构化通道剪枝判别依据视为一个优化问题，最小化剪枝后前后的代价函数之间的差。

四个要点:

1、优化方程是最小化已减去权重的代价函数与未剪枝之前权重的代价函数之差，用一阶泰勒展开式去近似优化方程，计算通道重要性只需要激活函数与对应的梯度的乘积，再求其均值；

2、对计算出来的重要性进行$\ell_{2}$归一化；

3、加入FLOPs等正则化，使其硬件更友好；

4、可以联合其他通道重要性判据

图片描述：三步剪枝流程图

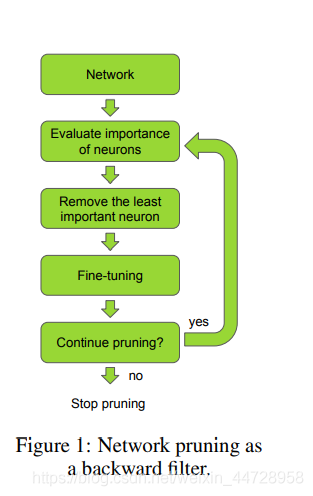
一.剪枝的优化方程¶

这一部分是为了推导出公式(6)、公式(7)和公式(8)。

训练样本集合 $\mathcal{D}=\{\mathcal{X}=$ $\left.\left\{\mathbf{x}_{0}, \mathbf{x}_{1}, \ldots, \mathbf{x}_{N}\right\}, \mathcal{Y}=\left\{y_{0}, y_{1}, \ldots, y_{N}\right\}\right\},$

$\mathbf{x}$ 表示输入，$y$ 表示输出

网络模型的参数 $\mathcal{W}=\left\{\left(\mathbf{w}_{1}^{1}, b_{1}^{1}\right),\left(\mathbf{w}_{1}^{2}, b_{1}^{2}\right), \ldots\left(\mathbf{w}_{L}^{C_{\ell}}, b_{L}^{C_{\ell}}\right)\right\}$

模型参数的代价函数为$\mathcal{C}(\mathcal{D} \mid \mathcal{W})$ ，其中 $\mathcal{C}(\cdot)$ 是负对数似然函数(negative log-likelihood function)

剪枝的目标是最小化已减去的权重的代价函数与未剪枝之前的代价函数的差，记为公式(1)：

$s.t. \quad\left\|\mathcal{W}^{\prime}\right\|_{0} \leq B$

其中 ，$\quad\left\|\mathcal{W}^{\prime}\right\|_{0}$ 是$\ell_{0}$范数，也即非0值的个数，$\mathcal{W}^{\prime}$ 是被剪掉的权重参数。

按照最朴素遍历的方法，剪去一组参数$\mathcal{W}$需要$2^{\mathcal{W}}$次计算，显然不科学的。比如VGG-16有4224个卷积特征图（可以对照VGG模型数出来）。

利用泰勒展开式的方法来近似优化方程：

一组卷积核：$(w, b) \in \mathcal{W}$

$\mathbf{z}_{\ell} \in \mathbb{R}^{H_{\ell} \times W_{\ell} \times C_{\ell}}$，$z_{\ell}$是一组$H_{\ell} * W_{\ell} * C_{\ell}$特征图， $\ell \in[1, 2, 3,...L]$表示layer

单张特征图$\mathbf{z}_{\ell}^{(k)},k \in [1, 2,3,..., C_{\ell}]$

$\mathbf{z}_{\ell}^{(k)}=\mathbf{g}_{\ell}^{(k)} \mathcal{R}\left(\mathbf{z}_{\ell-1} * \mathbf{w}_{\ell}^{(k)}+b_{\ell}^{(k)}\right)$

$\mathbf{g}_{l} \in\{0,1\}^{C}$,表示剪枝与否。

所以 $\mathcal{W}^{\prime}=\mathbf{g} \mathcal{W}$

特征图集合记为： $h=\left\{z_{0}^{(1)}, z_{0}^{(2)}, \ldots, z_{L}^{\left(C_{\ell}\right)}\right\}$

$h_{i}$是由一组参数$\mathcal{W_{i}}$得到的

$\mathcal{C}\left(\mathcal{D} \mid h_{i}\right)=\mathcal{C}\left(\mathcal{D} \mid(\mathbf{w}, b)_{i}\right)$

公式(2)

$\mathcal{C}\left(\mathcal{D}, h_{i}=0\right)$表示被剪去参数的代价函数 $ \mathcal{C}\left(\mathcal{D}, h_{i}\right)$是原来参数的代价函数

公式(3) 为泰勒公式： $$ f(x)=\sum_{p=0}^{P} \frac{f^{(p)}(a)}{p !}(x-a)^{p}+R_{p}(x), 在x = a处 $$

用一阶泰勒展开式来逼近$\Delta \mathcal{C}$，即$p=1$，

公式(4)：

余项采用拉格朗日（Lagrange）余项：

所以 $R_{1}\left(h_{i}=0\right)$ :

忽略余项，将公式(4)代入公式(2)，

公式(5)：

公式(6)：

其中 $M$是特征图向量的长度。公式5和公式6本质上没有什么区别，只是等价变换。

到这里，优化方程已经得到了，就是公式6，得出的就是通道重要性的评分，这里计算通道重要性只需要计算激活函数与对应的梯度的乘积，再求其均值。

另外，为了保证跨层的通道之间的公平性，对特征图作了$\ell_{2}$归一化，

公式(7)

其中$\Theta(\mathbf{z}_{l}^{(k)})$是第$\ell$层中第$k$个通道（参数组）的重要性。

最后一点，做了FLOPs正则化，这个是为了减少FLOPs，这里也可以对其他参数做正则化，比如存储大小，内存，卷积核。

公式(8)

二、核心代码实现¶

整个代码不算大，但是全部贴上来也占据不少位置，于是我就贴上文章核心观点的重要代码，全部代码在参考链接。

图片描述：整体代码流程图

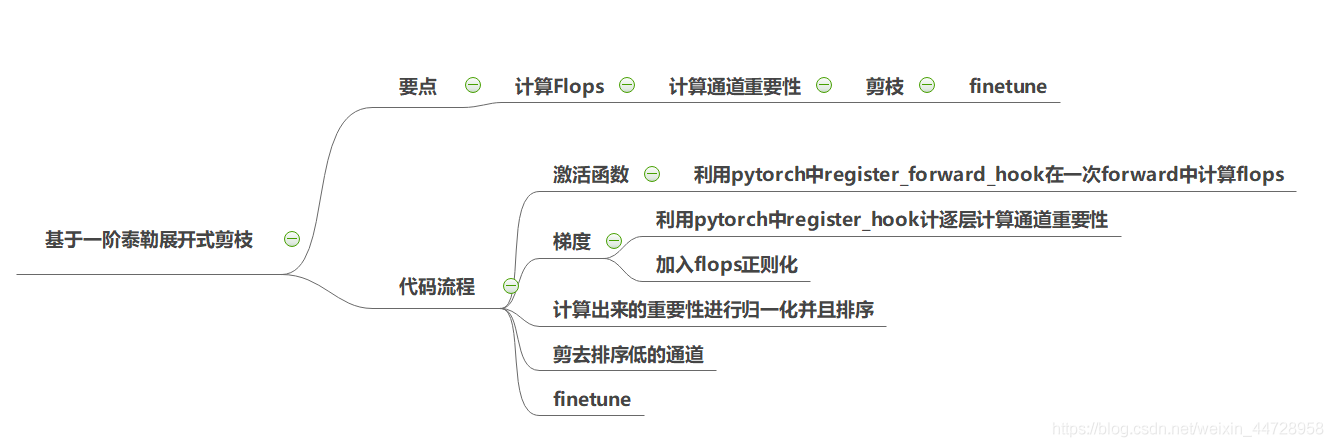
1、通道重要性计算

def compute_rank(self, grad, lamda=1):
    activation_index = len(self.activations) - self.grad_index - 1
    activation = self.activations[activation_index]

    taylor = activation * grad                  ##计算基于一阶泰勒展开的值   
    taylor = taylor.mean(dim=(0, 2, 3)).data    ## 以通道维度计算得分

    flops = self.flops_dict[activation_index] * torch.ones_like(taylor) ###FLOPs 正则化,见下面get_flops()
    taylor = taylor - lamda * flops # 公式(8)

    if activation_index not in self.filter_ranks:
        self.filter_ranks[activation_index] = torch.FloatTensor(activation.size(1)).zero_().cuda()

        self.filter_ranks[activation_index] += taylor
        self.grad_index += 1

2、计算FLOPs

def get_flops(self):
    self.flops_dict = {}
    def hook(module, inputs, outputs):  #hook函数，用来计算每层的flops
        params = module.weight.size().numel()  #torch.numel() 返回一个tensor变量内所有元素个数，可以理解为矩阵内元素的个数
        W = outputs.size(2)
        H = outputs.size(3)
        module.flops = params * W * H   #计算flops

    for m in model.modules():
        if isinstance(m, nn.Conv2d):
            m.register_forward_hook(hook) #为每一层注册hook
        x = torch.randn(1, 3, 224, 224) #随便定义一个数据，跑一次forward来获取flops
        _ = self.model(x)
        activation_index = 0
        for m in self.model.modules():
            if isinstance(m, nn.Conv2d):
                self.flops_dict[activation_index] = m.flops  #获取每层的flops，记录到字典
                activation_index += 1

3、对基于一阶泰勒展开式计算得到重要性，进行通道归一化

def normalize_ranks_per_layer(self):
    for i in self.filter_ranks:
        v = torch.abs(self.filter_ranks[i])
        v = v / torch.sqrt(torch.sum(v * v))
        self.filter_ranks[i] = v

三、文章的一些讨论¶

1、泰勒展开的讨论

1990年 LeCun提出Optimal Brain Damage (OBD) 也是采用泰勒展开式的方法来近似。因为经过多次训练迭代后，梯度会趋向于0，那么$y=\frac{\delta \mathcal{C}}{\delta h} h$，则$\mathbb{E}(y)=0$，所以LeCun认为$y$提供的信息很有限，$\mathcal{C}\left(\mathcal{D}, h_{i}\right)-\frac{\delta \mathcal{C}}{\delta h_{i}} h_{i}-\mathcal{C}\left(\mathcal{D}, h_{i}\right) =0$ ，所以采用泰勒二阶展开式。

虽然$y$的期望为0，但是他的方差不为0，其$\left |y \right |\neq 0$，所以$\mathbb{E}(\left |y \right |)\neq 0$，所以$\left|\mathcal{C}\left(\mathcal{D}, h_{i}\right)-\frac{\delta \mathcal{C}}{\delta h_{i}} h_{i}-\mathcal{C}\left(\mathcal{D}, h_{i}\right)\right|\neq 0$，可以用一阶泰勒展开式来近似。

2、通道重要性

虽然文章提出了一种基于一阶泰勒展开的方法计算通道重要性，从flops正则化中我们可以，将其他通道重要性判别也加入最后的重要性排序，也就是在公式8中加入其他项，这样可以更加全面的考虑通道重要性；当然，随之增加的就是整个剪枝算法的计算量和耗时也增加。

四、参考链接¶

• 论文：https://arxiv.org/abs/1611.06440

• 代码：https://github.com/azhe198827/channel_prune

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。