1. 前言¶
一般我们在构建CNN的时候都是以32位浮点数为主,这样在网络规模很大的情况下就会占用非常大的内存资源。然后我们这里来理解一下浮点数的构成,一个float32类型的浮点数由一个符号位,8个指数位以及23个尾数为构成,即:
符号位[ ] + 指数位[ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] + 尾数[ ]*23
我们可以看到,每个float32浮点数里面一共有2^{23}=83886087个二进制对应表示2^{23}个数,又10^6<2^{23}<10^8,所以我们一般可以精确地表示6位有效数字,但是无法表示8位有效数字。浮点数有正负所以需要一个符号位来表示,还有8个指数位来表示指数(指数也是要存储的)由于有正负也就是[-127,128]。
然后完成一个浮点数的加减运算至少有如下过程: - 检查操作数,即如果有一个参与运算的数为0,那么直接得出结果。 - 比较阶码大小完成对阶。 - 对尾数进行加或减运算。 - 将结果规格化并进行舍入处理。
关于这一节,可以看这个表述得非常清楚的博客:http://www.cppblog.com/jianjianxiaole/articles/float.html
从上面对浮点数的介绍来看,如果我们使用全浮点数的CNN,那么不仅仅会占用大量的内存,还需要大量的计算资源。在这种背景下,低比特量化的优势就体验出来了。接下来,我们就先看一下2016年NIPS提出的《Binarized Neural Networks: Training Neural Networks with Weights andActivations Constrained to +1 or −1》这篇论文,简称BNN,然后再对BNN的Pytorch代码做一个解析。
2. BNN的原理¶
2.1 二值化方案¶
在训练BNN时,我们要把网络层的权重和输出值设为1或者-1,下面是论文提出的2种二值化方法。
第一种是直接将大于等于0的参数设置为1,小于0的设置为-1,即:
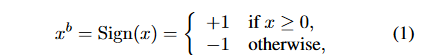
第二种是将绝对值大于1的参数设为1,将绝对值小于1的参数根据距离+/-1的远近按概率随机置为+/-1:
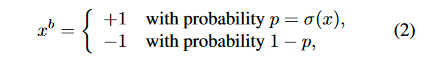
其中\sigma(x)是一个clip函数,公式如下:

论文中提到,第二种方法似乎更加合理,但它也引入了按概率分布的随机比特数,因此硬件实现会消耗很多时间,所以通常会选定第一种方法来对权重和输出值进行量化。
2.2 如何反向传播?¶
将CNN的权重和输出值二值化以后,梯度信息应当怎么办呢?论文指出梯度仍然不得不用较高精度的实数来存储,因为梯度很小,所以无法使用低精度来正确表达梯度,同时梯度是有高斯白噪声的,累加梯度才能抵消噪声。另外,二值化相当于给权重和输出值添加了噪声,这种噪声具有正则化的作用,可以防止模型过拟合,即它可以让权重更加稀疏。
由于sign函数的导数在非0处都是0,所以在梯度回传的时候使用tanh来替代sign进行求导,这里假设损失函数是C,输入是r,对r做二值化可得:
q=sign(r)
C对q的导数可以用g_q表示,那么C对r的导数为:
g_r=g_q1_{|r|<=1}
其中1_{|r|<=1}是tanh的梯度,这样就可以进行梯度回传,然后就可以根据梯度不断优化并训练参数了。
这里需要注意的是我们需要使用BatchNorm层,BN层最大的作用就是可以加速学习并减少权重尺度的影响,带来一定量的正则化并提高CNN的性能,但是BN设计了很多的矩阵运算会降低运算速度。因此,论文提出了一种Shift-based Batch Normalization(SBN)层。SBN的优点是几乎不需要矩阵运算,并且不会带来性能损失。SBN的操作过程如下:

这个函数实现了在不使用乘法的情况下近似计算BN,可以提高计算效率。
同样也是为了加速二值网络的训练,改进了AdaMax优化器。具体算法如下图所示。

2.3 第一层怎么办?¶
由于网络除了输入以外,全部都是二值化的,所以需要对第一层进行处理,将其二值化,整个二值化网络的处理流程如下:

整个过程可以表示为:初始化第一层->计算前一层点积的Xnor->计算BatchNorm的符号->执行网络到倒数第二层->计算输出...
以上是假设输入的每个数字只有8位的情况,如果我们希望使用任意n位的整数,那么我们可以对公式进行推广,即:
LinearQuant(x,bitwidth)=clip(round(\frac{x}{bitwidth})\times bitwidth, minV, maxV)
或者
LogQuant(x,bitwidth)=clip(AP2(x), minV, maxV)
3. 代码实现¶
接下来我们来解析一下Pytorch实现一个BNN,需要注意的是代码实现和上面介绍的原理有很多不同,首先第一个卷积层没有做二值化,也就是说第一个卷积层是普通的卷积层。对于输入也没有做定点化,即输入仍然为Float。另外,对于BN层和优化器也没有按照论文中的方法来做优化,代码地址如下:https://github.com/666DZY666/model-compression/blob/master/quantization/WbWtAb/models/nin.py
3.1 定义网络结构¶
下面的代码定义了支持权重和输出值分别可选二值或者三值量化,可以看到核心函数即为Conv2d_Q。
import torch.nn as nn
from .util_wt_bab import Conv2d_Q
# *********************量化(三值、二值)卷积*********************
class Tnn_Bin_Conv2d(nn.Module):
# 参数:last_relu-尾层卷积输入激活
def __init__(self, input_channels, output_channels,
kernel_size=-1, stride=-1, padding=-1, groups=1, last_relu=0, A=2, W=2):
super(Tnn_Bin_Conv2d, self).__init__()
self.A = A
self.W = W
self.last_relu = last_relu
# ********************* 量化(三/二值)卷积 *********************
self.tnn_bin_conv = Conv2d_Q(input_channels, output_channels,
kernel_size=kernel_size, stride=stride, padding=padding, groups=groups, A=A, W=W)
self.bn = nn.BatchNorm2d(output_channels)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
x = self.tnn_bin_conv(x)
x = self.bn(x)
if self.last_relu:
x = self.relu(x)
return x
class Net(nn.Module):
def __init__(self, cfg = None, A=2, W=2):
super(Net, self).__init__()
# 模型结构与搭建
if cfg is None:
cfg = [192, 160, 96, 192, 192, 192, 192, 192]
self.tnn_bin = nn.Sequential(
nn.Conv2d(3, cfg[0], kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(cfg[0]),
Tnn_Bin_Conv2d(cfg[0], cfg[1], kernel_size=1, stride=1, padding=0, A=A, W=W),
Tnn_Bin_Conv2d(cfg[1], cfg[2], kernel_size=1, stride=1, padding=0, A=A, W=W),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
Tnn_Bin_Conv2d(cfg[2], cfg[3], kernel_size=5, stride=1, padding=2, A=A, W=W),
Tnn_Bin_Conv2d(cfg[3], cfg[4], kernel_size=1, stride=1, padding=0, A=A, W=W),
Tnn_Bin_Conv2d(cfg[4], cfg[5], kernel_size=1, stride=1, padding=0, A=A, W=W),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
Tnn_Bin_Conv2d(cfg[5], cfg[6], kernel_size=3, stride=1, padding=1, A=A, W=W),
Tnn_Bin_Conv2d(cfg[6], cfg[7], kernel_size=1, stride=1, padding=0, last_relu=1, A=A, W=W),
nn.Conv2d(cfg[7], 10, kernel_size=1, stride=1, padding=0),
nn.BatchNorm2d(10),
nn.ReLU(inplace=True),
nn.AvgPool2d(kernel_size=8, stride=1, padding=0),
)
def forward(self, x):
x = self.tnn_bin(x)
x = x.view(x.size(0), -1)
return x
3.2 具体实现¶
我们跟进一下Conv2d_Q函数,来看一下二值化的具体代码实现,注意我将代码里面和三值化有关的部分省略了。
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Function
# ********************* 二值(+-1) ***********************
# A 对激活值进行二值化的具体实现,原理中的第一个公式
class Binary_a(Function):
@staticmethod
def forward(self, input):
self.save_for_backward(input)
output = torch.sign(input)
return output
@staticmethod
def backward(self, grad_output):
input, = self.saved_tensors
#*******************ste*********************
grad_input = grad_output.clone()
#****************saturate_ste***************
grad_input[input.ge(1)] = 0
grad_input[input.le(-1)] = 0
'''
#******************soft_ste*****************
size = input.size()
zeros = torch.zeros(size).cuda()
grad = torch.max(zeros, 1 - torch.abs(input))
#print(grad)
grad_input = grad_output * grad
'''
return grad_input
# W 对权重进行二值化的具体实现
class Binary_w(Function):
@staticmethod
def forward(self, input):
output = torch.sign(input)
return output
@staticmethod
def backward(self, grad_output):
#*******************ste*********************
grad_input = grad_output.clone()
return grad_input
# ********************* A(特征)量化(二值) ***********************
# 因为我们使用的网络结构不是完全的二值化,第一个卷积层是普通卷积接的ReLU激活函数,所以要判断一下
class activation_bin(nn.Module):
def __init__(self, A):
super().__init__()
self.A = A
self.relu = nn.ReLU(inplace=True)
def binary(self, input):
output = Binary_a.apply(input)
return output
def forward(self, input):
if self.A == 2:
output = self.binary(input)
# ******************** A —— 1、0 *********************
#a = torch.clamp(a, min=0)
else:
output = self.relu(input)
return output
# ********************* W(模型参数)量化(三/二值) ***********************
def meancenter_clampConvParams(w):
mean = w.data.mean(1, keepdim=True)
w.data.sub(mean) # W中心化(C方向)
w.data.clamp(-1.0, 1.0) # W截断
return w
# 对激活值进行二值化
class weight_tnn_bin(nn.Module):
def __init__(self, W):
super().__init__()
self.W = W
def binary(self, input):
output = Binary_w.apply(input)
return output
def forward(self, input):
# **************************************** W二值 *****************************************
output = meancenter_clampConvParams(input) # W中心化+截断
# **************** channel级 - E(|W|) ****************
E = torch.mean(torch.abs(output), (3, 2, 1), keepdim=True)
# **************** α(缩放因子) ****************
alpha = E
# ************** W —— +-1 **************
output = self.binary(output)
# ************** W * α **************
output = output * alpha # 若不需要α(缩放因子),注释掉即可
# **************************************** W三值 *****************************************
else:
output = input
return output
# ********************* 量化卷积(同时量化A/W,并做卷积) ***********************
class Conv2d_Q(nn.Conv2d):
def __init__(
self,
in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
A=2,
W=2
):
super().__init__(
in_channels=in_channels,
out_channels=out_channels,
kernel_size=kernel_size,
stride=stride,
padding=padding,
dilation=dilation,
groups=groups,
bias=bias
)
# 实例化调用A和W量化器
self.activation_quantizer = activation_bin(A=A)
self.weight_quantizer = weight_tnn_bin(W=W)
def forward(self, input):
# 量化A和W
bin_input = self.activation_quantizer(input)
tnn_bin_weight = self.weight_quantizer(self.weight)
#print(bin_input)
#print(tnn_bin_weight)
# 用量化后的A和W做卷积
output = F.conv2d(
input=bin_input,
weight=tnn_bin_weight,
bias=self.bias,
stride=self.stride,
padding=self.padding,
dilation=self.dilation,
groups=self.groups)
return output
上面的代码比较好理解,因为它将BNN论文中最难实现的SBN和改进后的AdaMax优化算法省略掉了,并且没有对输入进行定电化,所以编码难度小了很多,这个代码可以验证一下使用BNN之后精度损失。
4. 实验结果¶
这里贴一下使用上面的网络训练Cifar10图像分类数据集的准确率对比:
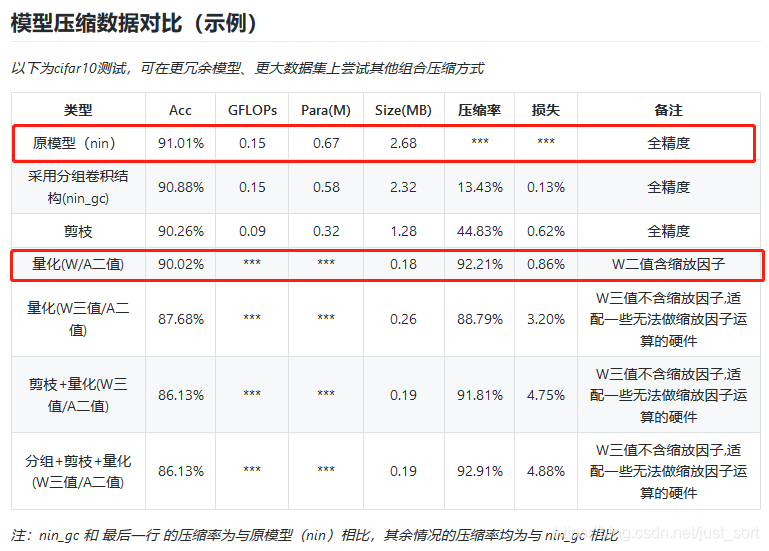
可以看到如果将除了第一层卷积之外的卷积层均换成二值化卷积之后,模型的压缩率高达92%并且准确率也只有1个点的下降,这说明在Cifar10数据集上这种方法确实是有效的。笔者跑了一下这个代码,测试结果和代码作者是类似的。
5. 思考¶
我们看一下论文给出的BNN在MNIST/CIFAR-10等数据集上的测试结果:
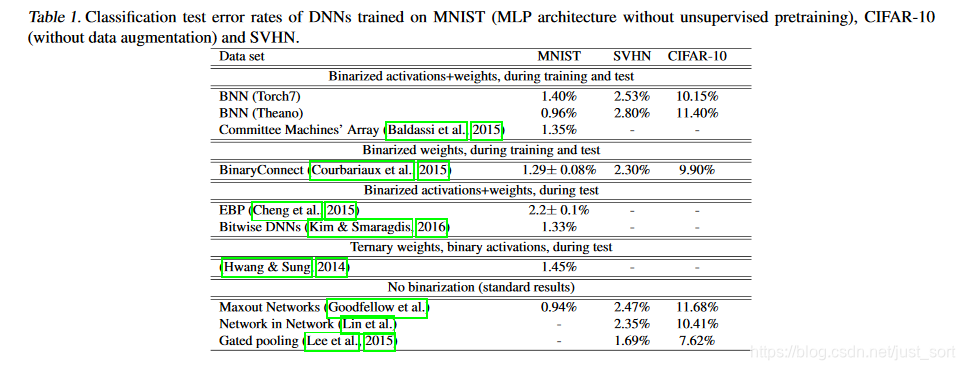
可以看到这些简单网络的分类误差还在可接受的范围之内,但这种二值化网络在ImageNet上的测试结果却是比较差的,出现了很大的误差。虽然还存在很多的优化技巧比如放开Tanh的边界,用2Bit的激活函数可以提升一些精度,但在复杂模型下效果仍然不太好。因此,二值化模型的最大缺点应该是不适合复杂模型。另外,新定义的算子在部署时也是一件麻烦的事,还需要专门的推理框架或者定制的硬件来支持。不然就只能像我们介绍的代码实现那样,使用矩阵乘法来模拟这个二值化计算过程,但加速是非常有限的。
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。

本文总阅读量次