介绍¶

在实现Sigmoid激活函数的时候，有一个exp(-x)的操作，这个函数是非常耗时的，但是在神经网络中一般权值是比较小的，那么就有了这种快速计算算法。

算法原理¶

在神经网络中，当x比较小时， $e^x$ 会逼近一个极限：

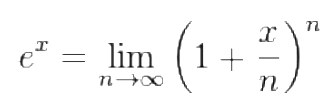
在这里插入图片描述

,其中n可以取较大数，一般为2的整数幂次，比如取256，那么后面的 $1+\frac{x}{n}$ 就相乘8次。如果取1024，需要乘以10次。这个极限和math.h的exp的精度比较为：

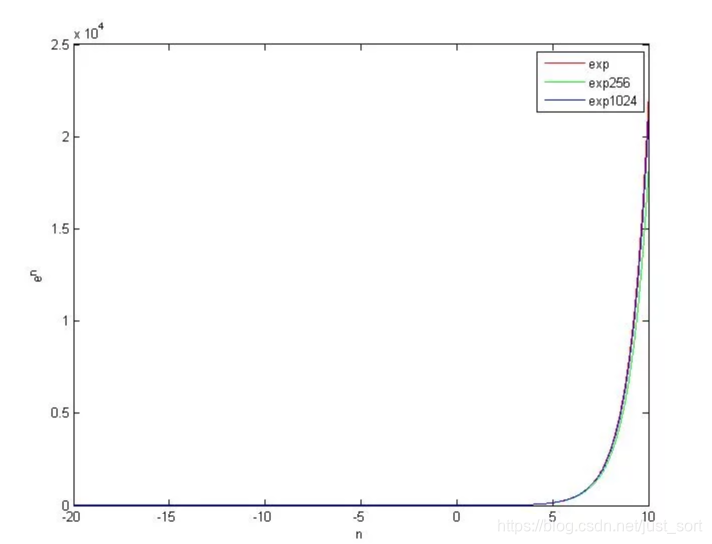
在这里插入图片描述

可以看到在数据不超过7~8的时候，函数的计算结果几乎是一致的。速度方面exp256是原始exp的360倍，exp1024是原始exp的330倍，相比之下exp1024比exp256 handle的范围稍大。

代码实现¶

inline float exp1(float x) {
    x = 1.0 + x / 256.0;
    x *= x; x *= x; x *= x; x *= x;
    x *= x; x *= x; x *= x; x *= x;
    return x;
}

inline float exp2(double x) { 
    x = 1.0 + x / 1024;   
    x *= x; x *= x; x *= x; x *= x;   
    x *= x; x *= x; x *= x; x *= x;   
    x *= x; x *= x;   
    return x; 
}

本文总阅读量次