INT8 量化训练

【GiantPandaCV 导读】本文聊了两篇做 INT8 量化训练的文章，量化训练说的与 quantization-aware Training 有区别，量化训练指的是在模型训练的前向传播和后向传播都有 INT8 量化。两篇文章都是基于对梯度构建分析方程求解得到解决量化训练会引起的训练崩溃和精度损失严重的情况。

论文：《Distribution Adaptive INT8 Quantization for Training CNNs》 会议：AAAI 2021

论文：《Towards Unified INT8 Training for Convolutional Neural Network》 会议：CVPR 2020

引言：什么是量化训练

谷歌在 2018 年《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference》文章中，提出了量化感知训练 (Quantization-aware Training，QAT)，QAT 只在前向传播中，加入模拟量化，这个模型量化指的是把模型参数进行线性量化，然后在做矩阵运算之前，把之前量化的模型参数反量化回去浮点数。而量化训练则是在前向传播和后向传播都加入量化，而且做完矩阵运算再把运算的结果反量化回去浮点数。 《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference》详细的内容在链接中：

MXNet 实现卷积神经网络训练量化

Pytorch 实现卷积神经网络训练量化 (QAT)

一、Distribution Adaptive INT8

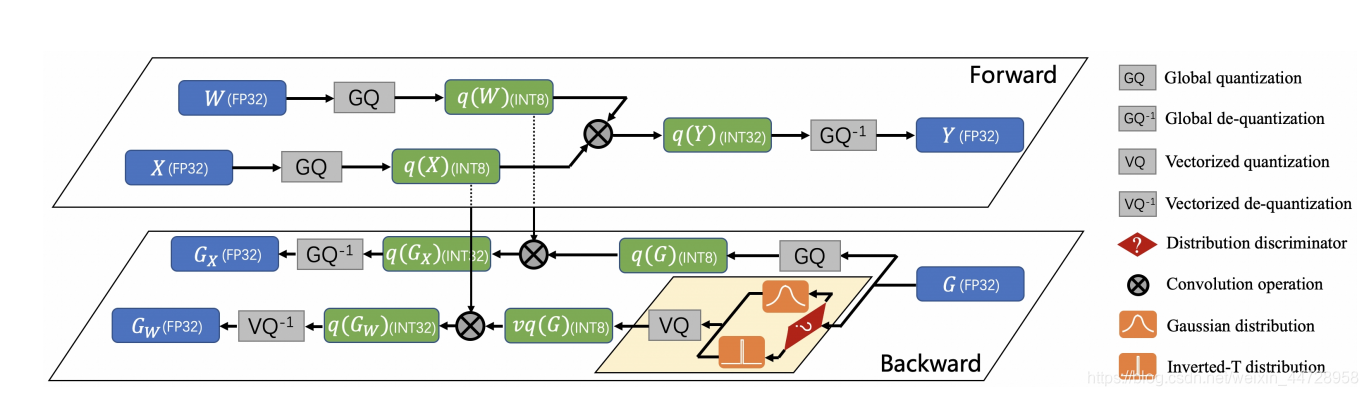
文章的核心 idea 是：Unified INT8 发现梯度的分布不遵从一个分布即不能像权重一样归于高斯分布，Distribution Adaptive INT8 认为梯度可以 channel-wise 看，分成两种分布，一个高斯分布，一个是倒 T 形分布，这样去 minimize 量化后梯度与原来梯度的量化误差 Error，就可以了。 Unified INT8 也是类似 minimize 量化后梯度与原来梯度的量化误差 Error 的思想，与 Distribution Adaptive INT8 不同的是通过收敛性分析方程，发现可以通过降低学习率和减少梯度量化误差。 总结：Distribution Adaptive INT8 比 Unified INT8 多了一个先验，来构建分析方程。方法上，都是对梯度下手，修正梯度的值，都有对梯度进行截断。

Distribution Adaptive INT8 采用了两个方法：Gradient Vectorized Quantization 和 Magnitude-aware Clipping Strategy。

对称量化：

$q(x)=\operatorname{round}\left(127 \cdot \frac{\operatorname{clamp}(x, s)}{s}\right) (1)$

$\operatorname{clamp}(x, s)=\left\{\begin{array}{ll} x, & |x| \leq s \\ \operatorname{sign}(x) \cdot s, & |x|>s \end{array}\right.$

这里， $s$ 是阈值范围，就是 range $[-s, s]$

反量化： $\hat{x}=q(x) \times \frac{s}{127}$

公式 (1) 与之前常见的对称量化长的有一点不一样：

$q=\operatorname{round}\left(\frac{\operatorname{clip}(x, c)}{s}\right)$ (2)

$\operatorname{clip}(\mathrm{x}, \mathrm{c})=\min (\max (\mathrm{x},-\mathrm{c}), \mathrm{c}), s=\frac{c}{2^{8-1}-1}$

反量化： $\hat{x}=q(x) \times s$ , 这里的 s 指的是 scale，c 是 clipping 阈值

其实公式 (1) 和(2)是等价变化，把公式 (2) 的 s 计算出来，就是 $s=\frac{c}{127}$ ，代入公式 (2)

也就是等于公式 (1)

Gradient Vectorized Quantization：

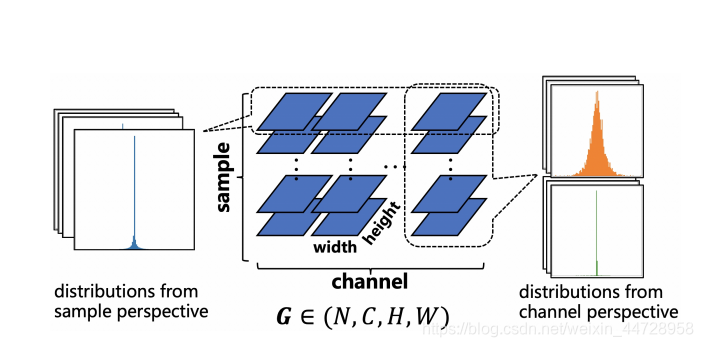
这就是 channel-wise 的筛选哪些梯度的分布属于高斯分布还是倒 T 分布 (a sharp with long-tailed shape distribution(Inverted-T distribution))。

所以这两种分布： $\left\{\begin{array}{l} p \sim N\left(\mu, \sigma^{2}\right), P(|g|>\sigma)>\lambda \\ p \sim T^{-1}, \quad P(|g|>\sigma) \leq \lambda \end{array}\right.$

$\lambda$ 通过实验设置为 0.3

Magnitude-aware Clipping Strategy：

这个 cliiping 是在寻找最优截断阈值 s

量化误差分析： $E=\int_{g_{\min }}^{g_{\max }}|g-\hat{g}| f(g) p(g) d g$（3）

$f(g)=e^{\alpha|g|}，p(g)$ 是梯度的分布。

通过两个假设：

$\begin{array}{l} \forall g \in \mathbb{R}, p(g)=p(-g) \\ \forall g \in(0, s),|g-\hat{g}| \approx \frac{1}{2} \cdot \frac{s}{127} \end{array}$，误差分析方差变换为：

$E=\underbrace{\int_{0}^{s} \frac{s}{127} \cdot f(g) p(g) d g}_{I 1}+\underbrace{2 \int_{s}^{g_{\max }}(g-s) \cdot f(g) p(g) d g}_{I 2}$

只要求导 $\left.\frac{\partial E}{\partial s}\right|_{s=\bar{s}}=0$ 就可以找出找出最优值 $\bar{s}$ 。然后分不同的梯度的分布进行讨论。

对于高斯分布：$\bar{s}=|g|_{\max }$

对于倒 T 分布：倒 T 分布用分段均匀分布来表示

$p_{T^{-1}}(g)=\left\{\begin{array}{ll} a, & |g| \in(0, \epsilon) \\ b, & |g| \in\left(\epsilon,|g|_{\max }\right) \end{array}\right.$

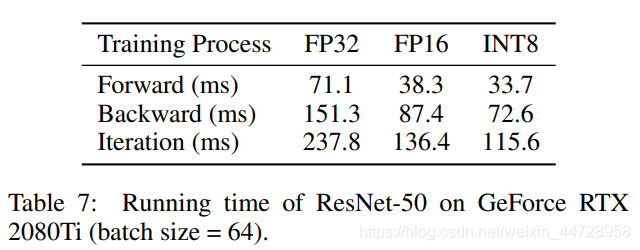
经过一顿公式推导得出： $\bar{s}_{t}=(1-k A) \bar{s}_{t-1}+A|g|_{\max , t}$ ，引进了 $k$ 和 $A$ 这两个超参数。

所以 $k=1$ 和 $A=0.8$

整个 Distribution Adaptive INT8 的 pipeline：

SpeedUp:

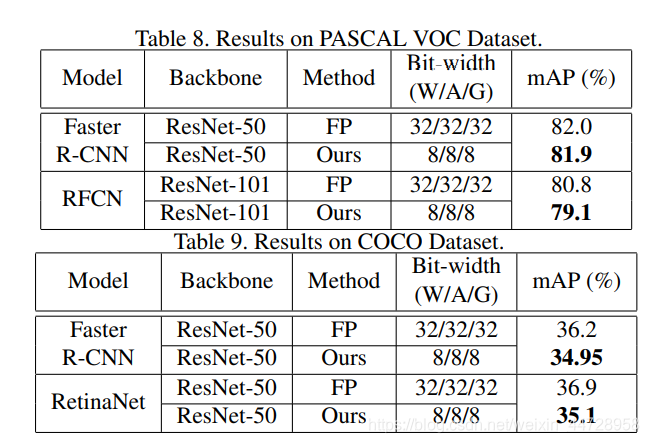
实验：

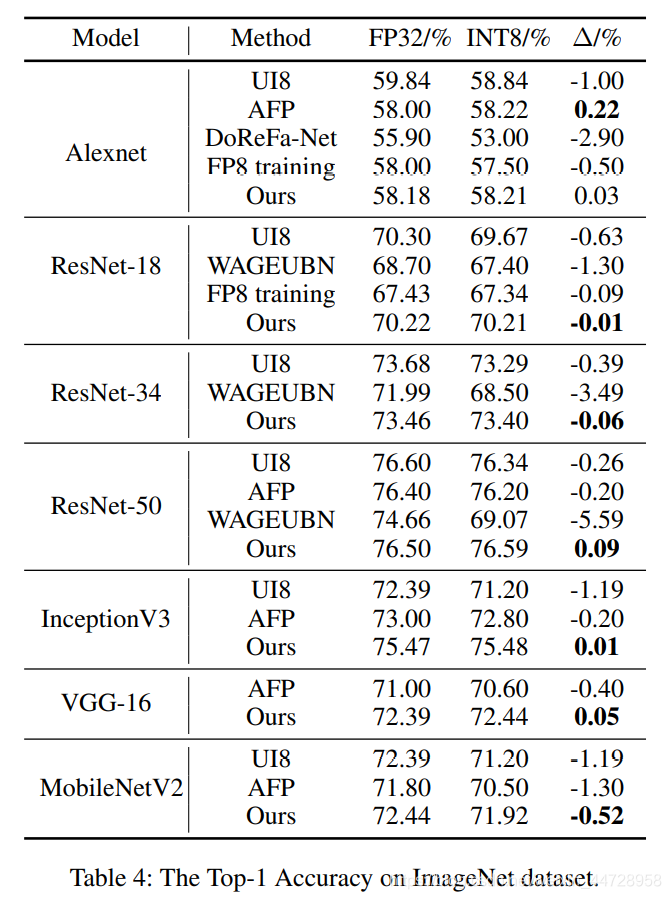
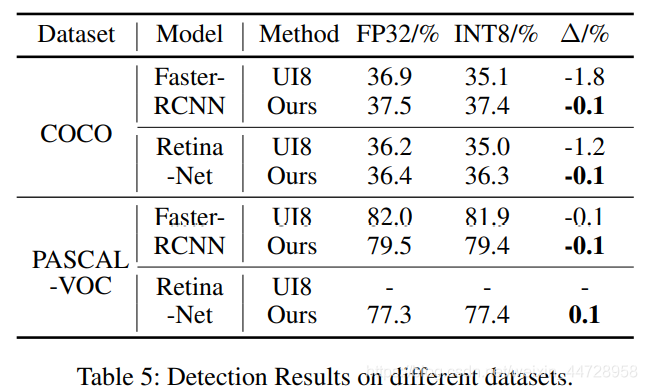
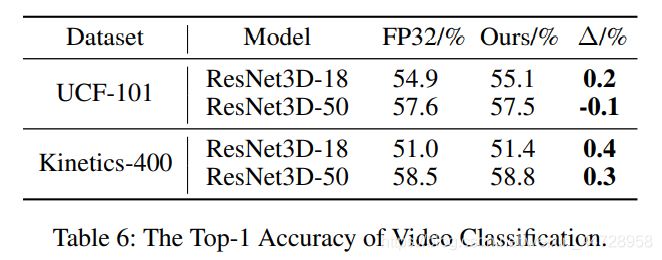
二、Unified INT8 Training

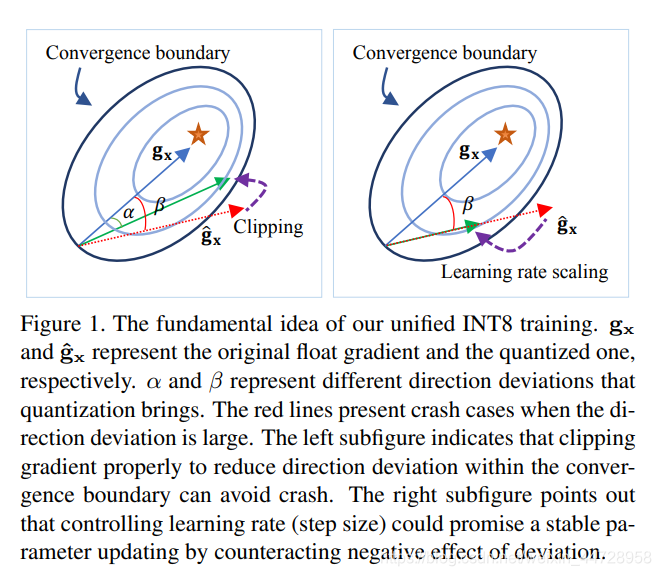
前面已经讲了 Unified INT8 的整体思路了。Unified INT8 也是类似 minimize 量化后梯度与原来梯度的量化误差 Error 的思想，Unified INT8 是通过收敛性分析方程，发现了可以通过降低学习率和减少梯度量化误差。另外，Unified INT8 对梯度误差分析是 layer-wise 的，即不是上述 Distribution Adaptive INT8 那种 channel-wise 的方式。

通过收敛性证明： $R(T)=\sum_{t=1}^{T}\left(f_{t}\left(\mathbf{w}_{t}\right)-f_{t}\left(\mathbf{w}^{*}\right)\right)$ (4)

基于这两个假设： $\begin{aligned} &f_{t} \text { is convex; }\\ &\forall \mathbf{w}_{i}, \mathbf{w}_{j} \in \mathbb{S},\left\|\mathbf{w}_{i}-\mathbf{w}_{j}\right\|_{\infty} \leq D_{\infty} \end{aligned}$

公式 (4) 变换为：

$\frac{R(T)}{T} \leq \underbrace{\frac{d D_{\infty}^{2}}{2 T \eta_{T}}}_{(1)}+\underbrace{\frac{D_{\infty}}{T} \sum_{t=1}^{T}\left\|\epsilon_{t}\right\|}_{(2)}+\underbrace{\frac{1}{T} \sum_{t=1}^{T} \frac{\eta_{t}}{2}\left\|\hat{\mathbf{g}}_{t}\right\|^{2}}_{(3)}$

因为 T 是迭代次数，T 会不断增大，导致 Term(1) 趋向于 0；

$\epsilon_{t}$ 是误差，Term(2) 说明，要最小化量化误差；

$\eta_{t}$ 是量化 - 反量化后的梯度， $\eta_{t}$ 是学习率，Term(3) 说明要降低学习率。

所以 Unified INT8 提出两个方法：Direction Sensitive Gradient Clipping 和 Direction Sensitive Gradient Clipping。

Direction Sensitive Gradient Clipping：

$d_{c}=1-\cos (<\mathbf{g}, \hat{\mathbf{g}}>)=1-\frac{\mathbf{g} \cdot \hat{\mathbf{g}}}{|\mathbf{g}| \cdot|\hat{\mathbf{g}}|}$

用余弦距离来度量量化前后梯度的偏差。

Deviation Counteractive Learning Rate Scaling：

$\phi\left(d_{c}\right)=\max \left(e^{-\alpha d_{c}}, \beta\right)$

这两个策略最终的用在了调整学习率，实验得出，$\beta$ 取 0.1，$\alpha$ 取 20。

整个 pipeline：

SpeedUp:

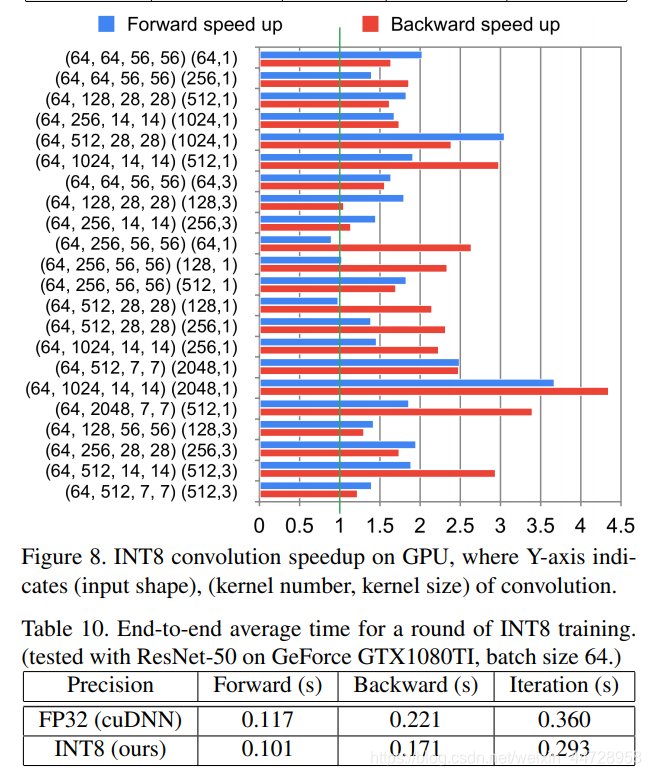
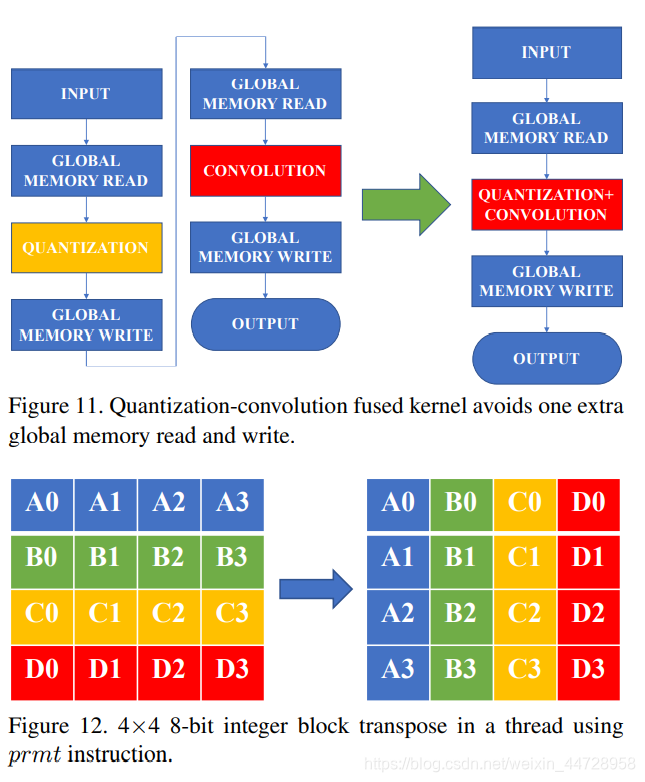
这里有个重要的 cuda 层的优化：

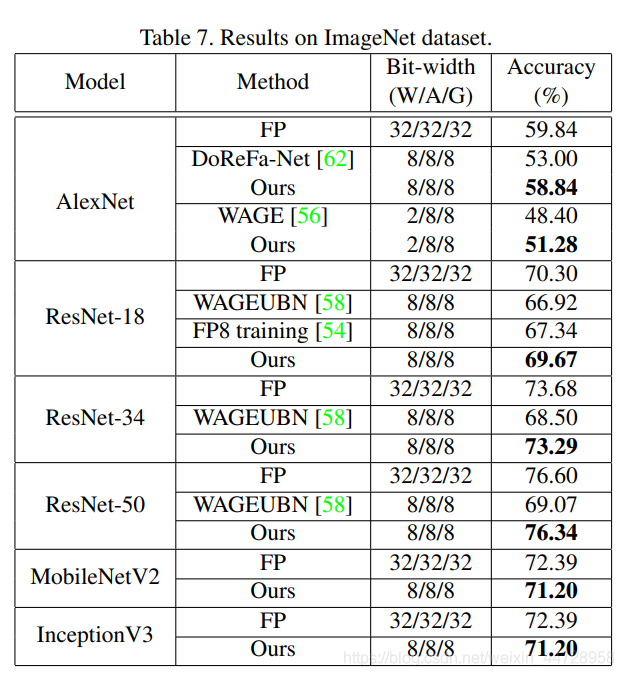
实验：

知乎链接：

（量化 | INT8 量化训练）https://zhuanlan.zhihu.com/p/364782854

欢迎关注 GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。(• ̀ω•́)✧

有对文章相关的问题，或者想要加入交流群，欢迎添加 BBuf 微信：