【GiantPandaCV】ThiNet是一种结构化剪枝,核心思路是找到一个channel的子集可以近似全集,那么就可以丢弃剩下的channel,对应的就是剪掉剩下的channel对应的filters。剪枝算法还是三步剪枝:train-prune-finetune,而且是layer by layer的剪枝。本文由作者授权首发于GiantPandaCV公众号。
0、 介绍¶
ThiNet是南京大学lamda实验室出品,是ICCV 2017的文章,文章全名《ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression》。
文章的主要思路是:ThiNet是基于filter剪枝,将filter剪枝操作形式化地定义为一个优化问题,通过下一层的统计信息来指导当前层的剪枝。如果移除当前层(记为l_{i})filter(记为W_{i}),那么 l_{i+1}层channel和W_{i}同样被丢弃;但是如果l_{i+1}层的filter的数量不变,则l_{i+1}层的输出(也是l_{i+2}层的输入)维度不变。也就是发现这样的剪枝对l_{i+1}层的输出(也是l_{i+2}层的输入)很小影响,作者提出ThiNet剪枝。 大白话就是找到一组channel的输出跟全部channel的输出之间的误差最小(采用均方误差/最小二乘法去衡量),那么就可以用这组channel来代替全部channel。
ThiNet剪枝流程:选择channel子集、剪枝、finetune,如下如图
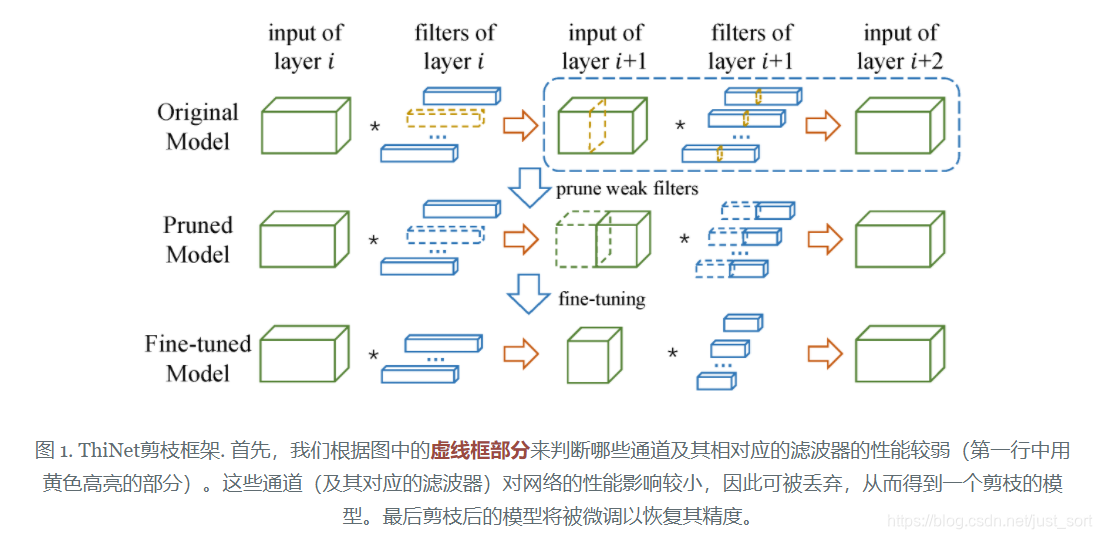
所以算法的实现的核心在于如何进行channel选择,一个channel是一个filter的计算结果,所以二者相互对应。
ThiNet有三个要点:
1、如何进行通道选择,通道的子集与全部通道的全集之间的最小二次乘法误差来做通道重要性判断依据
2、最小化重构误差,相当于给finetune一个初始化卷积核参数
3、对残差网络的剪枝做了适配
一、通道选择(channel selection)¶
文章采用贪心算法选择channel子集(也就是留下来的filter)。ThiNet是迭代式layer by layer的剪枝。
思路1(正向思路):根据通道重要性判断找到重要的channel,保留下来,然后迭代式剪枝进进行直到压缩率达到预设要求,见公式5。
为什么会有思路1?因为论文的主要思路是,找到一组channel的子集可以近似该层channel的全集,那么就是要找到可以留下来的channel,对应的就是该channel对应的filter;这就是论文的正向思路。
思路1的方法会有一个问题就是,留下来filter的数量是从大到小的变化的,那么按照思路1计算量会很大,因为留下来的filter(记为S)在剪枝一开始的时候要比被移除的filter(记为T)多,所以有
思路2:根据通道重要性判断找到要剪枝(丢弃)的filter,然后迭代式剪枝进行直到压缩率达到预设要求(丢弃一定数量的filter),见公式6。
ThiNet通道重要性判断是:找到一组通道子集近似通道全集的结果。
下面公式1-5我是根据论文写的,会有点绕,但对复现这篇论文不是那么重要,核心思路就是上面提到选取一部分channel来近似。
公式1:
公式2:
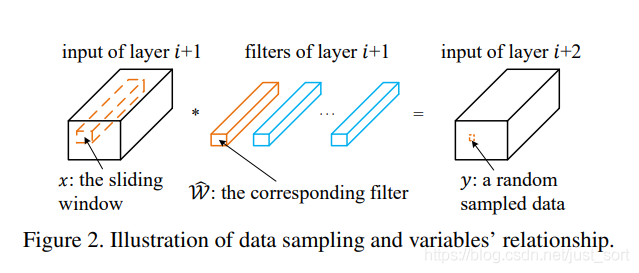
其中,\mathcal{I}_{i} \in \mathbb{R}^{C \times H \times W}是第i_{i}层输入张量,
y是从\mathcal{I}_{i+2}中随机采样得到的,
\mathcal{W}_{i} \in \mathbb{R}^{D \times C \times K \times K}是 K \times K 卷积核的集合,
x \in \mathcal{R}^{C \times K \times K}是对应\mathcal{W}_{i}的滑动窗口,
C 是channels, H 是行, W 是列,D是输出的通道数, b是bias
公式1和公式2,可以简化为公式3:
\hat{y}=\sum_{c=1}^{C} \hat{x}_{c}, \hat{y}=y-b
公式1~3是为了简化公式表示的等效变换。
基于通道在\hat{\mathbf{x}}=\left(\hat{x}_{1}, \hat{x}_{2}, \ldots, \hat{x}_{C}\right)中是独立的,\hat x只取决于x_{c,:,:},不依赖于x_{c^{\prime},:,:}, c^{\prime} \neq c,则有
公式4:\hat{y}=\sum_{c \in S} \hat{x}_{c},S是channel的子集。
公式5是为了最小化留下来的channel的计算结果与原来channel全集的计算结果,即为思路1:
变为公式6,即为思路2:
其中,S ∪ T = {1, 2, . . . , C},S ∩ T = ∅,r是压缩率,C是filter数量。
基于贪心算法选择filter子集的算法如图:

def channel_selection(inputs, module, sparsity=0.5, method='greedy'):
"""
选择当前模块的输入通道,以及高度重要的通道。
找到可以使现有输出最接近的输入通道。
:param inputs: torch.Tensor, input features map
:param module: torch.nn.module, layer
:param sparsity: float, 0 ~ 1 how many prune channel of output of this layer
:param method: str, how to select the channel
:return:
list of int, indices of channel to be selected and pruned
"""
num_channel = inputs.size(1) # 通道数
num_pruned = int(math.ceil(num_channel * sparsity)) # 输入需要删除的通道数
num_stayed = num_channel - num_pruned
print('num_pruned', num_pruned)
if method == 'greedy':
indices_pruned = []
while len(indices_pruned) < num_pruned:
min_diff = 1e10
min_idx = 0
for idx in range(num_channel):
if idx in indices_pruned:
continue
indices_try = indices_pruned + [idx]
inputs_try = torch.zeros_like(inputs)
inputs_try[:, indices_try, ...] = inputs[:, indices_try, ...]
output_try = module(inputs_try)
output_try_norm = output_try.norm(2) #这里就是公式6
if output_try_norm < min_diff:
min_diff = output_try_norm
min_idx = idx
indices_pruned.append(min_idx)
indices_stayed = list(set([i for i in range(num_channel)]) - set(indices_pruned))
inputs = inputs.cuda()
module = module.cuda()
return indices_stayed, indices_pruned
二、最小化重构误差(Minimize the reconstruction error)¶
首先先来看看numpy.linalg.lstsq(),是线性矩阵方程的最小二乘法求解。
最小二乘法的公式为:
| 方法 | 描述 |
|---|---|
| linalg.lstsq(a, b[, rcond]) | 返回线性矩阵方程的最小二乘解 |
numpy.linalg.lstsq(a, b, rcond='warn')
# 将least-squares解返回线性矩阵方程。
\hat{\mathbf{w}}=\underset{\mathbf{w}}{\arg \min } \sum_{i=1}^{m}\left(\hat{y}_{i}-\mathbf{w}^{\mathrm{T}} \hat{\mathbf{x}}_{i}^{*}\right)^{2}
其中, \hat{\mathbf{x}}_{i} 是通道选择后的训练样本,可以通过\hat{\mathbf{w}}=\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \mathbf{y} 求解
该方法是每一个通道赋予权重来进一步地减小重构误差。文章说这相当于给finetune一个很好的初始化。
def weight_reconstruction(module, inputs, outputs, use_gpu=False):
"""
reconstruct the weight of the next layer to the one being pruned
:param module: torch.nn.module, module of the this layer
:param inputs: torch.Tensor, new input feature map of the this layer
:param outputs: torch.Tensor, original output feature map of the this layer
:param use_gpu: bool, whether done in gpu
:return: void
"""
if module.bias is not None:
bias_size = [1] * outputs.dim()
bias_size[1] = -1
outputs -= module.bias.view(bias_size) # 从 output feature 中减去 bias (y - b)
if isinstance(module, torch.nn.Conv2d):
unfold = torch.nn.Unfold(kernel_size=module.kernel_size, dilation=module.dilation,
padding=module.padding, stride=module.stride)
unfold.eval()
x = unfold(inputs) # 展开到以一个面片(reception field)为列的三维数组 (N * KKC * L (number of fields))
x = x.transpose(1, 2) # transpose (N * KKC * L) -> (N * L * KKC)
num_fields = x.size(0) * x.size(1)
x = x.reshape(num_fields, -1) # x: (NL * KKC)
y = outputs.view(outputs.size(0), outputs.size(1), -1) # 将一个特征映射展开为一行数组 (N * C * WH)
y = y.transpose(1, 2) # transpose (N * C * HW) -> (N * HW * C), L == HW
y = y.reshape(-1, y.size(2)) # y: (NHW * C), (NHW) == (NL)
if x.size(0) < x.size(1) or use_gpu is False:
x, y = x.cpu(), y.cpu()
#上面一系列的reshape的操作是为了调用np.linalg.lstsq这个函数,利用最小二乘法求解weight
param, residuals, rank, s = np.linalg.lstsq(x.detach().cpu().numpy(),y.detach().cpu().numpy(),rcond=-1)
param = param[0:x.size(1), :].clone().t().contiguous().view(y.size(1), -1)
if isinstance(module, torch.nn.Conv2d):
param = param.view(module.out_channels, module.in_channels, *module.kernel_size)
del module.weight
module.weight = torch.nn.Parameter(param)
三、对于VGG-16的ThiNet剪枝策略¶
1、对前面10层剪枝力度大,因为前面10层的feature map比较大,FLOPs占据了超过90%
2、全连接层占据了 86.41%的模型参数,所以将其改成global average pooling layer
3、剪枝是layer by layer,每剪完一个layer finetune一个epoch,学习率设为0.001,到最后一层剪完 finetune 12个epoch,学习率设为0.0001.
4、在Imagenet上, VGG更具体的剪枝细节可以看论文4.2部分。
四、对于ResNet的剪枝策略¶
对于残差块的剪枝,因为有个add的操作,相加时候维度必须保持一致,所以残差块最后一层输出的filter不改变而只剪枝前面两层,如下所示:
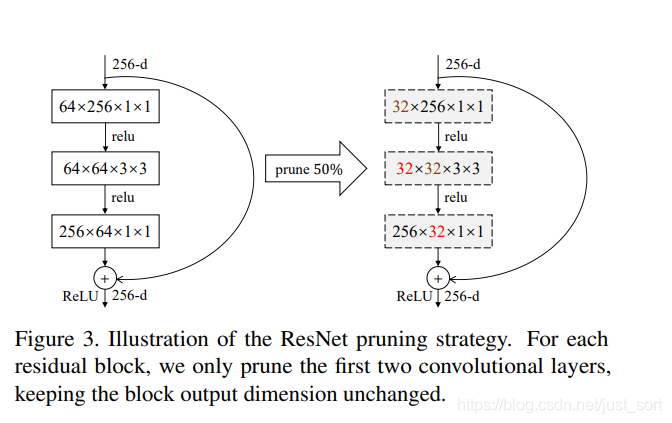
每剪完一个layer finetune一个epoch,固定学习率为0.0001,到最后一层剪完 finetune 9个epoch ,学习率从0.001到0.00001变换,其余的与VGG-16中一样。ResNet更具体细节,请查看论文4.3部分
五、参考链接¶
原作中文解读:http://www.lamda.nju.edu.cn/luojh/project/ThiNet_ICCV17/ThiNet_ICCV17_CN.html
论文:https://arxiv.org/abs/1707.06342
代码:https://github.com/Roll920/ThiNet
https://github.com/kkeono2/Channel-Pruning-using-Thinet-LASSO-
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。

本文总阅读量次