欢迎关注AI PC端算法优化代码库：https://github.com/BBuf/Image-processing-algorithm-Speed 。

0. 资源获取¶

公众号输入 高性能计算 关键词获取刘文志大佬的《并行编程方法与优化实践》电子书以及我整理的SSE指令集PDF。

1. 前言¶

终于下定决心来更新这个专题了，首先说一下我想做什么？我想做的就是基于SSE/AVX的PC端算法优化，也可以理解为对传统的OpenCV算法的指令集优化。这个系列也会保持一直更新，不断分享我学习SSE/AVX指令集以及利用它优化的一些小算法，希望能在算法加速这块帮助到一些人。

另外，虽然这个专题的核心是SSE/AVX算法优化，但我也会介绍一些其它的优化技术比如循环展开，多线程，内存优化，汇编优化等。

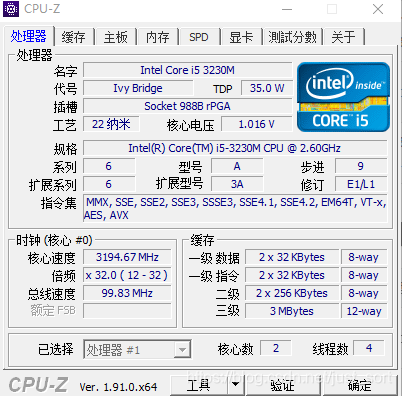
我们可以用CPU-Z这个软件来查询我们的Intel CPU支持哪些指令集，在我的笔记本上截图如下：

可以看到CPU支持哪些指令集

2. SSE/AVX介绍¶

下面的介绍来自刘文志大佬的并行编程方法与优化实践一书，这应该是做优化的同学最好的入门书籍之一了。

SSE/AVX是Intel公司设计的，对其X86体系的SIMD扩展指令集，它基于SIMD向量化技术，提高了X86硬件的计算能力，增强了X86多核向量处理器的图像和视频处理能力。

SSE/AVX指令支持向量化数据并行，一个指令可以同时对多个数据进行操作，同时操作的数据个数由向量寄存器的长度和数据类型共同决定。例如，SSE4向量寄存器(xmm)长度为128位，即16个字节，如果操作float或int的数据，可同时操作4个，如果操作char数据，可同时操作16个。而AVX向量寄存器(ymm)长度为256位，即32字节，如果操作char类型数据，可以同时操作32个，潜在地大幅度提升程序性能。注意，AVX也是支持128位的，大家可以在官方文档查看：https://software.intel.com/sites/landingpage/IntrinsicsGuide/#techs=AVX

直观点来看就是，当我们用最普通的方法去实现一个算法的时候，我们一般只能在某一时刻操作一个float/int/char数据。而引入了SSE/AVX指令集之后，我们可以同时操作多个数据，这自然提高了程序运行的效率。

Intel ICC和开源的GCC编译器支持的SSE/AVX指令的C接口(intrinsic，内置函数)声明在intrinsic.h头文件中。其数据类型命名主要有__m128/__m256，__m128d/__m256i，默认为单精度(d表示双精度，i表示整形)。其函数命名可大致分成3个使用_隔开的部分，3个部分的含义如下：

第一个部分为_mm或_mm256。_mm表示其为SSE指令，操作的向量长度为64位或128位。_mm256表示AVX指令，操作的向量长度为256位。
第二个部分为操作函数名称，如_add，_load，_mul等，一些函数操作会增加修饰符，比如loadu表示不对齐到向量长度的存储器访问。
第三个部分为操作的对象名及数据类型，_ps表示操作向量中所有的单精度数据。_pd表示操作向量中所有的双精度数据。_pixx表示操作向量中所有的xx位的有符号整型数据，向量寄存器长度为64位。_epixx表示操作向量中所有的xx位的有符号整型数据，向量寄存器长度为128位。_epuxx表示操作向量中所有的xx位的无符号整形数据，向量寄存器长度为128位。_ss表示只操作向量中第一个单精度数据。_si128表示操作向量寄存器中第一个128位的有符号整型数据。

这3个部分结合起来就构成了一个向量函数，如_mm256_add_ps表示使用256位向量寄存器执行单精度浮点加法运算。

Intel 指令集

3. AVX编程基础¶

3.1 数据类型¶

数据类型	描述
__m128	包含4个float类型数字的向量
__m128d	包含2个double类型数字的向量
__m128i	包含若干个整型数字的向量
__m256	包含8个float类型数字的向量
__m256d	包含4个double类型数字的向量
__m256i	包含若干个整型数字的向量

每一种类型，从2个下划线开头，接一个m，然后是v向量的位长度。
如果向量类型是以d结束的，那么向量里面是double类型的数字。如果没有后缀，就代表向量只包含float类型的数字。
整形的向量可以包含各种类型的整形数，例如char,short,unsigned long long。也就是说，__m256i可以包含32个char，16个short类型，8个int类型，4个long类型。这些整形数可以是有符号类型也可以是无符号类型。

3.2 函数命名约定¶

_mm<bit_width>_<name>_<data_type> - <bit_width> 表明了向量的位长度，对于128位的向量，这个参数为空，对于256位的向量，这个参数为256。 - <name>描述了内联函数的算术操作。 - <data_type> 标识函数主参数的数据类型。 - ps 包含float类型的向量 - pd 包含double类型的向量 - epi8/epi16/epi32/epi64 包含8位/16位/32位/64位的有符号整数 - epu8/epu16/epu32/epu64 包含8位/16位/32位/64位的无符号整数 - si128/si256 未指定的128位或者256位向量 - m128/m128i/m128d/m256/m256i/m256d 当输入向量类型与返回向量的类型不同时，标识输入向量类型

3.3 初始化函数¶

数据类型	描述
_mm256_setzero_ps/pd	返回一个全0的float类型的向量
_mm256_setzero_si256	返回一个全0的整形向量
_mm256_set1_ps/pd	用一个float类型的数填充向量
_mm256_set1_epi8/epi16/epi32/epi64x	用整形数填充向量
_mm256_set_ps/pd	用8个float或者4个double类型数字初始化向量
_mm256_set_epi8/epi16/epi32/epi64x	用一个整形数初始化向量
_mm256_set_m128/m128d/m128i	用2个128位的向量初始化一个256位向量
_mm256_setr_ps/pd	用8个float或者4个double的转置顺序初始化向量
_mm256_setr_epi8/epi16/epi32/epi64x	用若干个整形数的转置顺序初始化向量

3.4 从内存中加载数据¶

数据类型	描述
_mm256_load_ps/pd	从对齐的内存地址加载浮点向量
_mm256_load_si256	从对齐的内存地址加载整形向量
_mm256_loadu_ps/pd	从未对齐的内存地址加载浮点向量
_mm256_loadu_si256	从未对齐的内存地址加载整形向量
_mm_maskload_ps/pd	根据掩码加载128位浮点向量的部分
_mm256_maskload_ps/pd	根据掩码加载256位浮点向量的部分
(2)_mm_maskload_epi32/64	根据掩码加载128位整形向量的部分
(2)_mm256_maskload_epi32/64	根据掩码加载256位整形向量的部分
最后2个函数前面有一个(2)，代表这两个函数只在AVX2中支持。

3.5 加减法¶

数据类型	描述
_mm256_add_ps/pd	对两个浮点向量做加法
_mm256_sub_ps/pd	对两个浮点向量做减法
(2)_mm256_add_epi8/16/32/64	对两个整形向量做加法
(2)_mm256_sub_epi8/16/32/64	对两个整形向量做减法
(2)_mm256_adds_epi8/16 (2)_mm256_adds_epu8/16	两个整数向量相加且考虑内存饱和问题
(2)_mm256_subs_epi8/16 (2)_mm256_subs_epu8/16	两个整数向量相减且考虑内存饱和问题
_mm256_hadd_ps/pd	水平方向上对两个float类型向量做加法
_mm256_hsub_ps/pd	垂直方向上最两个float类型向量做减法
(2)_mm256_hadd_epi16/32	水平方向上对两个整形向量做加法
(2)_mm256_hsub_epi16/32	水平方向上最两个整形向量做减法
(2)_mm256_hadds_epi16	对两个包含short类型的向量做加法且考虑内存饱和的问题
(2)_mm256_hsubs_epi16	对两个包含short类型的向量做减法且考虑内存饱和的问题
_mm256_addsub_ps/pd	加上和减去两个float类型的向量

将饱和度考虑在内的函数将结果钳制到可以存储的最小/最大值。没有饱和的函数在饱和发生时忽略内存问题。

而在水平方向上做加减法的意思如下图：

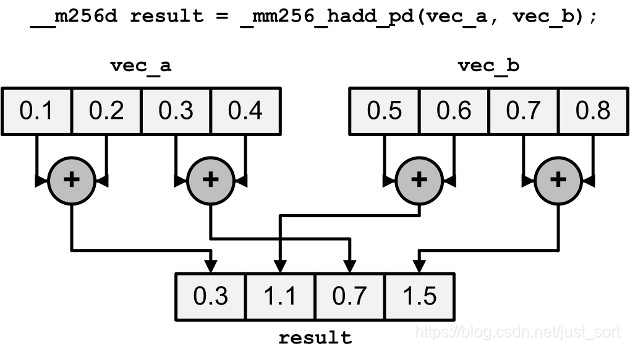
在水平方向上做加减法

最后一个指令：_mm256_addsub_ps/pd 在偶数位置减去，奇数位置加上，获最后得目标向量。

3.6 乘除法¶

数据类型	描述
_mm256_mul_ps/pd	对两个float类型的向量进行相乘
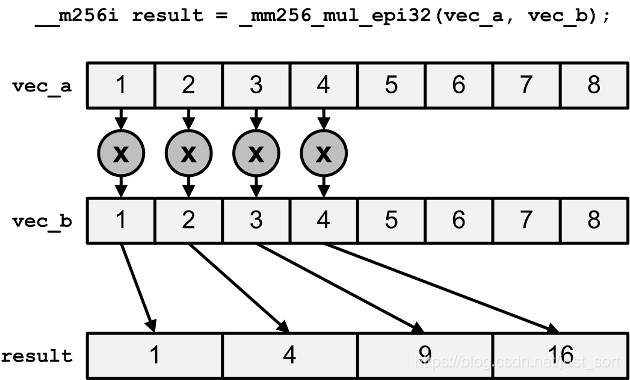
(2)_mm256_mul_epi32 (2)_mm256_mul_epu32	将包含32位整数的向量的最低四个元素相乘
(2)_mm256_mullo_epi16/32	整数相乘，低位存储
(2)_mm256_mulhi_epi16 (2)_mm256_mulhi_epu16	整数相乘，高位存储
(2)_mm256_mulhrs_epi16	16位数相乘得到32位数
_mm256_div_ps/pd	对两个float类型的向量进行相除

将包含32位整数的向量的最低四个元素相乘，AVX2指令

整数相乘，低位存储

3.7 融合乘法和加法¶

数据类型	描述
(2)_mm_fmadd_ps/pd/ (2)_mm256_fmadd_ps/pd	将两个向量相乘，再将积加上第三个。(res=a*b+c)
(2)_mm_fmsub_ps/pd/ (2)_mm256_fmsub_ps/pd	将两个向量相乘，然后从乘积中减去一个向量。(res=a*b-c)
(2)_mm_fmadd_ss/sd	将向量中最低的元素相乘并相加（res[0]=a[0]*b[0]+c[0])
(2)_mm_fmsub_ss/sd	将向量中最低的元素相乘并相减（res[0]=a[0]*b[0]-c[0])
(2)_mm_fnmadd_ps/pd (2)_mm256_fnmadd_ps/pd	将两个向量相乘，并将负积加到第三个。(res = -(a * b) + c)
(2)_mm_fnmsub_ps/pd/ (2)_mm256_fnmsub_ps/pd	将两个向量相乘，并将负积加到第三个 (res = -(a * b) - c)
(2)_mm_fnmadd_ss/sd	将两个向量的低位相乘，并将负积加到第三个向量的低位。(res[0] = -(a[0] * b[0]) + c[0])
(2)_mm_fnmsub_ss/sd	将最低的元素相乘，并从求反的积中减去第三个向量的最低元素。(res[0] = -(a[0] * b[0]) - c[0])
(2)_mm_fmaddsub_ps/pd/ (2)_mm256_fmaddsub_ps/pd	将两个矢量相乘，然后从乘积中交替加上和减去（res=a*b±c)
(2)_mm_fmsubadd_ps/pd/ (2)_mmf256_fmsubadd_ps/pd	将两个向量相乘，然后从乘积中交替地进行减法和加法（res=a*b-/+c）（奇数次方，偶数次方）

3.8 排列¶

数据类型	描述
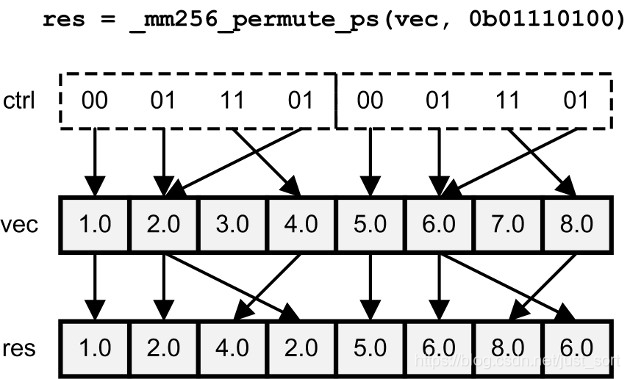
_mm_permute_ps/pd _mm256_permute_ps/pd	根据8位控制值从输入向量中选择元素
(2)_mm256_permute4x64_pd/ (2)_mm256_permute4x64_epi64	根据8位控制值从输入向量中选择64位元素
_mm256_permute2f128_ps/pd	基于8位控制值从两个输入向量中选择128位块
_mm256_permute2f128_si256	基于8位控制值从两个输入向量中选择128位块
_mm_permutevar_ps/pd _mm256_permutevar_ps/pd	根据整数向量中的位从输入向量中选择元素
(2)_mm256_permutevar8x32_ps (2)_mm256_permutevar8x32_epi32	使用整数向量中的索引选择32位元素（浮点数和整数）

根据8位控制值从输入向量中选择元素

3.9 Shuffle¶

数据类型	描述
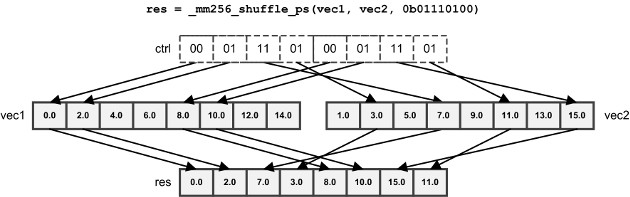
_mm256_shuffle_ps/pd	根据8位值选择浮点元素
_mm256_shuffle_epi8/ _mm256_shuffle_epi32	根据8位值选择整数元素
(2)_mm256_shufflelo_epi16/ (2)_mm256_shufflehi_epi16	基于8位控制值从两个输入向量中选择128位块

对于_mm256_shuffle_pd，只使用控制值的高4位。如果输入向量包含int或float，则使用所有控制位。对于_mm256_shuffle_ps，前两对位从第一个矢量中选择元素，第二对位从第二个矢量中选择元素。

根据8位值选择浮点元素

所有的指令的作用以及延迟，带宽，以及汇编实现均可以在官方在线文档中查看，地址如下： https://software.intel.com/sites/landingpage/IntrinsicsGuide/#techs=AVX&expand=4155

4. SSE编程基础¶

介于篇幅原因，这里就不展开介绍SSE了，这部分我提供了2个PDF文档在公众号输入关键词 高性能计算 就可以获取了。

5. RGB转GRAY原理¶

RGB是依据人眼识别的颜色定义出的空间，可表示大部分颜色。是图像处理中最基本、最常用、面向硬件的颜色空间，是一种光混合的体系。

RGB颜色空间最常用的用途就是显示器系统，彩色阴极射线管,彩色光栅图形的显示器都使用R、G、B数值来驱动R、G、B 电子枪发射电子，并分别激发荧光屏上的R、G、B三种颜色的荧光粉发出不同亮度的光线，并通过相加混合产生各种颜色。扫描仪也是通过吸收原稿经反射或透射而发送来的光线中的R、G、B成分，并用它来表示原稿的颜色。

首先是RGB2GRAY，也就是彩色图转灰度图的算法。RGB值和灰度的转换，实际上是人眼对于彩色的感觉到亮度感觉的转换，这是一个心理学问题，有一个公式：

Gray = 0.299 $\times$ R + 0.587 $\times$ G + 0.114 $\times$ B。

6. RGB转GRAY最简单实现¶

void RGB2Y(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    for (int Y = 0; Y < Height; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Width;
        for (int X = 0; X < Width; X++, LinePS += 3) {
            LinePD[X] = int(0.114 * LinePS[0] + 0.587 * LinePS[1] + 0.299 * LinePS[2]);
        }
    }
}

分辨率	优化	循环次数	速度
4032x3024	原始实现	100	34.87ms

7. RGB转GRAY优化第一版¶

直接计算复杂度较高，考虑优化可以将小数转为整数，除法变为移位，乘法也变为移位，但是这种方法也会带来一定的精度损失，我们可以根据实际情况选择需要保留的精度位数。下面给出不同精度(2-20位)的计算公式：

Gray = (R*1 + G*2 + B*1) >> 2

Gray= (R*2 + G*5 + B*1) >> 3

Gray= (R*4 + G*10 + B*2) >> 4

Gray = (R*9 + G*19 + B*4) >> 5

Gray = (R*19 + G*37 + B*8) >> 6

Gray= (R*38 + G*75 + B*15) >> 7

Gray= (R*76 + G*150 + B*30) >> 8

Gray = (R*153 + G*300 + B*59) >> 9

Gray = (R*306 + G*601 + B*117) >> 10

Gray = (R*612 + G*1202 + B*234) >> 11

Gray = (R*1224 + G*2405 + B*467) >> 12

Gray= (R*2449 + G*4809 + B*934) >> 13

Gray= (R*4898 + G*9618 + B*1868) >> 14

Gray = (R*9797 + G*19235 + B*3736) >> 15

Gray = (R*19595 + G*38469 + B*7472) >> 16

Gray = (R*39190 + G*76939 + B*14943) >> 17

Gray = (R*78381 + G*153878 + B*29885) >> 18

Gray =(R*156762 + G*307757 + B*59769) >> 19

Gray= (R*313524 + G*615514 + B*119538) >> 20

下面测试一下保留8位精度的代码实现和速度测试：

void RGB2Y_1(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    const int B_WT = int(0.114 * 256 + 0.5);
    const int G_WT = int(0.587 * 256 + 0.5);
    const int R_WT = 256 - B_WT - G_WT;
    for (int Y = 0; Y < Height; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Width;
        for (int X = 0; X < Width; X++, LinePS += 3) {
            LinePD[X] = (B_WT * LinePS[0] + G_WT * LinePS[1] + R_WT * LinePS[2]) >> 8;
        }
    }
}

分辨率	优化	循环次数	速度
4032x3024	原始实现	100	34.87ms
4032x3024	第一版优化	100	23.10ms

可以看到这一版优化将速度加速了接近10ms，还是比较可观的。

8. RGB转Gray优化第二版¶

在第一版优化的基础上，使用4路并行，然后我们看看有没有进一步的加速效果。代码实现和速度测试如下：

void RGB2Y_2(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    const int B_WT = int(0.114 * 256 + 0.5);
    const int G_WT = int(0.587 * 256 + 0.5);
    const int R_WT = 256 - B_WT - G_WT; // int(0.299 * 256 + 0.5)
    for (int Y = 0; Y < Height; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Width;
        int X = 0;
        for (; X < Width - 4; X += 4, LinePS += 12) {
            LinePD[X + 0] = (B_WT * LinePS[0] + G_WT * LinePS[1] + R_WT * LinePS[2]) >> 8;
            LinePD[X + 1] = (B_WT * LinePS[3] + G_WT * LinePS[4] + R_WT * LinePS[5]) >> 8;
            LinePD[X + 2] = (B_WT * LinePS[6] + G_WT * LinePS[7] + R_WT * LinePS[8]) >> 8;
            LinePD[X + 3] = (B_WT * LinePS[9] + G_WT * LinePS[10] + R_WT * LinePS[11]) >> 8;
        }
        for (; X < Width; X++, LinePS += 3) {
            LinePD[X] = (B_WT * LinePS[0] + G_WT * LinePS[1] + R_WT * LinePS[2]) >> 8;
        }
    }
}

分辨率	优化	循环次数	速度
4032x3024	原始实现	100	34.87ms
4032x3024	第一版优化	100	23.10ms
4032x3024	第二版优化	100	17.76ms

可以看到采用了4路并行之后速度也稍有提高。

9. RGB2Gray优化第三版¶

这一版优化即今天的核心内容，基于SSE指令集对RGB2Gray进行优化，在讲解原理之前先放出代码以及速度测试，后面对应着源码更容易懂原理。

void RGB2Y_3(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    const int B_WT = int(0.114 * 256 + 0.5);
    const int G_WT = int(0.587 * 256 + 0.5);
    const int R_WT = 256 - B_WT - G_WT; // int(0.299 * 256 + 0.5)

    for (int Y = 0; Y < Height; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Width;
        int X = 0;
        for (; X < Width - 12; X += 12, LinePS += 36) {
            __m128i p1aL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 0))), _mm_setr_epi16(B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT)); //1
            __m128i p2aL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 1))), _mm_setr_epi16(G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT)); //2
            __m128i p3aL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 2))), _mm_setr_epi16(R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT)); //3

            __m128i p1aH = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 8))), _mm_setr_epi16(R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT));//4
            __m128i p2aH = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 9))), _mm_setr_epi16(B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT));//5
            __m128i p3aH = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 10))), _mm_setr_epi16(G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT));//6

            __m128i p1bL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 18))), _mm_setr_epi16(B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT));//7
            __m128i p2bL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 19))), _mm_setr_epi16(G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT));//8
            __m128i p3bL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 20))), _mm_setr_epi16(R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT));//9

            __m128i p1bH = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 26))), _mm_setr_epi16(R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT));//10
            __m128i p2bH = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 27))), _mm_setr_epi16(B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT));//11
            __m128i p3bH = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 28))), _mm_setr_epi16(G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT));//12

            __m128i sumaL = _mm_add_epi16(p3aL, _mm_add_epi16(p1aL, p2aL));//13
            __m128i sumaH = _mm_add_epi16(p3aH, _mm_add_epi16(p1aH, p2aH));//14
            __m128i sumbL = _mm_add_epi16(p3bL, _mm_add_epi16(p1bL, p2bL));//15
            __m128i sumbH = _mm_add_epi16(p3bH, _mm_add_epi16(p1bH, p2bH));//16
            __m128i sclaL = _mm_srli_epi16(sumaL, 8);//17
            __m128i sclaH = _mm_srli_epi16(sumaH, 8);//18
            __m128i sclbL = _mm_srli_epi16(sumbL, 8);//19
            __m128i sclbH = _mm_srli_epi16(sumbH, 8);//20
            __m128i shftaL = _mm_shuffle_epi8(sclaL, _mm_setr_epi8(0, 6, 12, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1));//21
            __m128i shftaH = _mm_shuffle_epi8(sclaH, _mm_setr_epi8(-1, -1, -1, 18, 24, 30, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1));//22
            __m128i shftbL = _mm_shuffle_epi8(sclbL, _mm_setr_epi8(-1, -1, -1, -1, -1, -1, 0, 6, 12, -1, -1, -1, -1, -1, -1, -1));//23
            __m128i shftbH = _mm_shuffle_epi8(sclbH, _mm_setr_epi8(-1, -1, -1, -1, -1, -1, -1, -1, -1, 18, 24, 30, -1, -1, -1, -1));//24
            __m128i accumL = _mm_or_si128(shftaL, shftbL);//25
            __m128i accumH = _mm_or_si128(shftaH, shftbH);//26
            __m128i h3 = _mm_or_si128(accumL, accumH);//27
            //__m128i h3 = _mm_blendv_epi8(accumL, accumH, _mm_setr_epi8(0, 0, 0, -1, -1, -1, 0, 0, 0, -1, -1, -1, 1, 1, 1, 1));
            _mm_storeu_si128((__m128i *)(LinePD + X), h3);//28
        }
        for (; X < Width; X++, LinePS += 3) {//29
            LinePD[X] = (B_WT * LinePS[0] + G_WT * LinePS[1] + R_WT * LinePS[2]) >> 8;//30
        }
    }
}

分辨率	优化	循环次数	速度
4032x3024	原始实现	100	34.87ms
4032x3024	第一版优化	100	23.10ms
4032x3024	第二版优化	100	17.76ms
4032x3024	第三版(SSE)优化	100	10.54ms

可以看到SSE优化还是很给力的，相对于原始的实现，已经提速了3倍多，接下来我们来看看这段代码实现的原理。

算法原理：

首先，代码一次性处理12个像素，每个像素有BGR三个值，我们将BGR序列写出来看看：

B1 G1 R1 B2 G2 R2 B3 G3 R3 B4 G4 R4 B5 G5 R5 B6 G6 R6 B7 G7 R7 B8 G8 R8 B9 G9 R9 B10 G10 R10 B11 G11 R11 B12 G12 R12

我们知道SSE指令一次可以处理16个字节型数据，8个short类型数据以及4个int类型数据，由于这个程序中的数据运算结果不会超过short能表达的最大数值，所以这里使用short作为计算对象。然后我们使用SSE指令读取数据然后进行一些相乘操作，例如这几行代码：

__m128i p1aL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 0))), _mm_setr_epi16(B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT)); //1
__m128i p2aL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 1))), _mm_setr_epi16(G_WT, R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT)); //2
__m128i p3aL = _mm_mullo_epi16(_mm_cvtepu8_epi16(_mm_loadu_si128((__m128i *)(LinePS + 2))), _mm_setr_epi16(R_WT, B_WT, G_WT, R_WT, B_WT, G_WT, R_WT, B_WT)); //3

以及这行：

__m128i sumaL = _mm_add_epi16(p3aL, _mm_add_epi16(p1aL, p2aL));

就实现了以下过程：

如下过程为矩阵运算，其中加粗为对应位求和，为所求的灰度值

(B1 G1 R1 B2 G2 R2 B3 G3) x (B_WT G_WT R_WT B_WT G_WT R_WT B_WT G_WT) +

(G1 R1 B2 G2 R2 B3 G3 R3) x (G_WT R_WT B_WT G_WT R_WT B_WT G_WT R_WT) +

(R1 B2 G2 R2 B3 G3 R3 B4) x (R_WT B_WT G_WT R_WT B_WT G_WT R_WT B_WT) =

(B1 x B_WT + G1 x G_WT + R1 x R_WT) ，(G1 x G_WT + R1 x R_WT + B2 x B_WT) ， (R1 x R_WT + B2 x B_WT + G2 x G_WT) ，

(B2 x B_WT + G2 x G_WT + R2 x R_WT) ， (G2 x G_WT + R2 x R_WT + B3 x B_WT) ， (R2 x R_WT + B3 x B_WT + G3 x G_WT) ，

(B3 x B_WT + G3 x G_WT + R3 x R_WT) ， (G3 x G_WT + R3 x R_WT + B4 x B_WT)

上面得到了一个SSE的包含8个short类型的向量，其中加粗部分就是本次我们要的第一个答案（一共处理12个像素，现在处理了3个像素，得到了第一个答案）。注释后面标注的第1到16行都是相同的过程，核心原理即是把字节数据读入并和相应的权重相乘。接下来我们来分析以下一些关键指令：

_mm_loadu_si128就是把之后8个16个字节(short) 的数据读入到一个SSE寄存器中,注意由于任意位置的图像数据内存地址肯定不可能都满足SIMD16字节对齐的规定，因此这里不是用的_mm_load_si128指令。
_mm_cvtepu8_epi16指令则把这16个字节的低64位的8个字节数扩展为8个16位数据，这样做主要是为了上面所说的乘法做准备。如下所示：

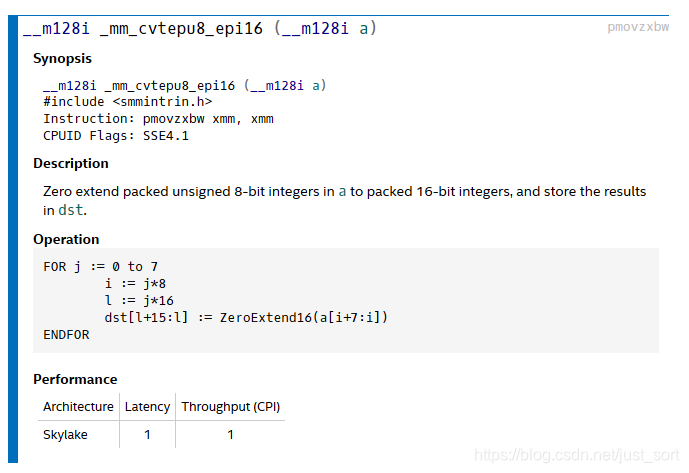
_mm_cvtepu8_epi16 指令

_mm_setr_epi16这个实际上就是用已知的8个16位数据来构造一个SSE向量。如下所示：

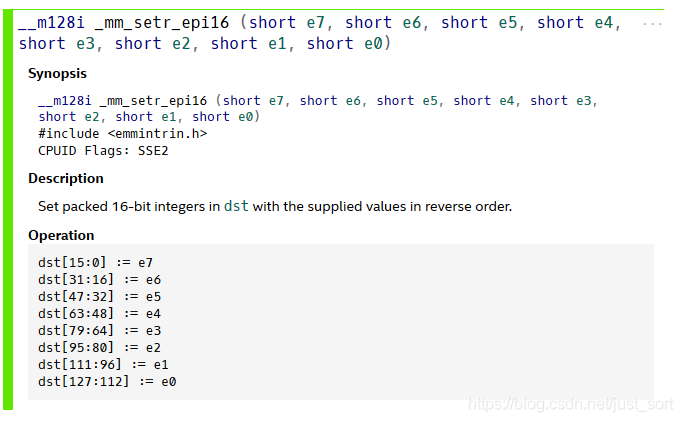
_mm_setr_epi16 指令

_mm_mullo_epi16 指令就是两个16位的乘法，注意不是用的_mm_mulhi_epi16，因为两个16位数相乘，一般要用32位数才能完整的保存结果，而_mm_mullo_epi16 是提取这个32位的低16位，我们这里前面已经明确了乘积的结果是不会超出short类型的，所以只取低16位就已经完全保留了所有的信息。这个指令的详细解释请看：

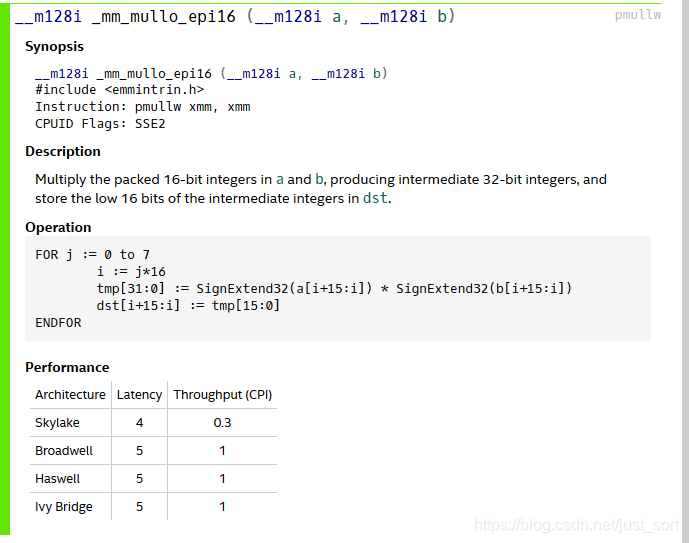
_mm_mulhi_epi16 指令

再对比一下_mm_mulhi_epi16：

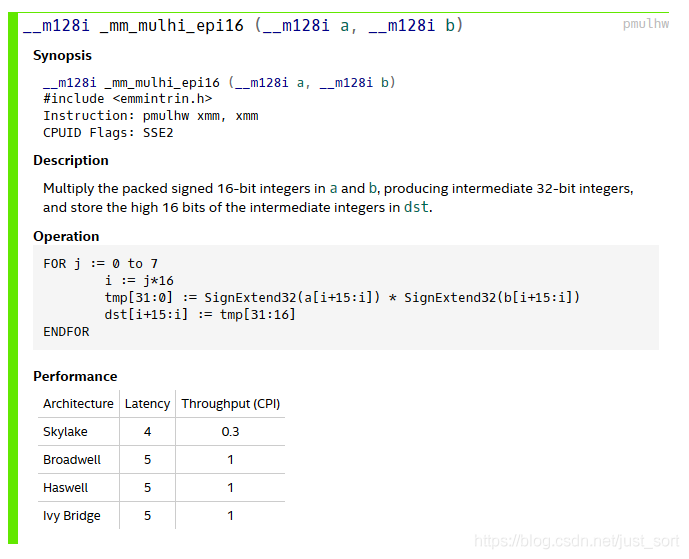
_mm_mulhi_epi16 指令

_mm_srli_epi16 这个就是移位操作，相当于普通算法中的>>8。
_mm_shuffle_epi8 把保存数字的位提到前面去，这样方便我们后面进行合并为一个完整的sse向量。举个例子，这里第一个变量的位置为什么是0,6,12呢，因为最后计算得到的变量高位是没有信息的，我们只使用了低8位，而sse中的内存排布大概是这样子：

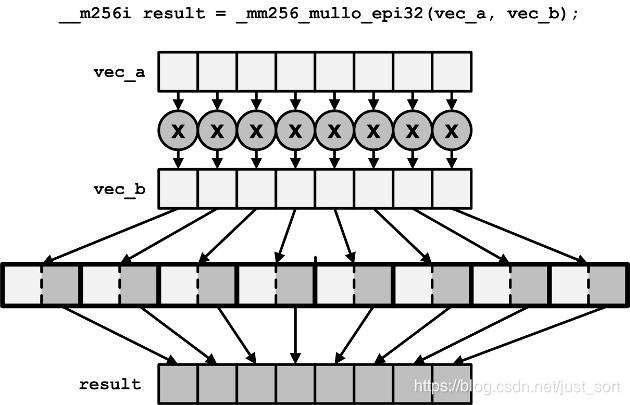
SSE向量的内存排布

可以把黑色的看成低位，所以这里下标是0,6,12，而不是想当然的0,3,6。为-1的部分都会变为0。

到这里，我们已经计算出来了所有的目标值，接下来就将其组合成一个SSE向量进行存储就行了。这里组合有两种方式实现，一种是利用_mm_blendv_epi8指令：

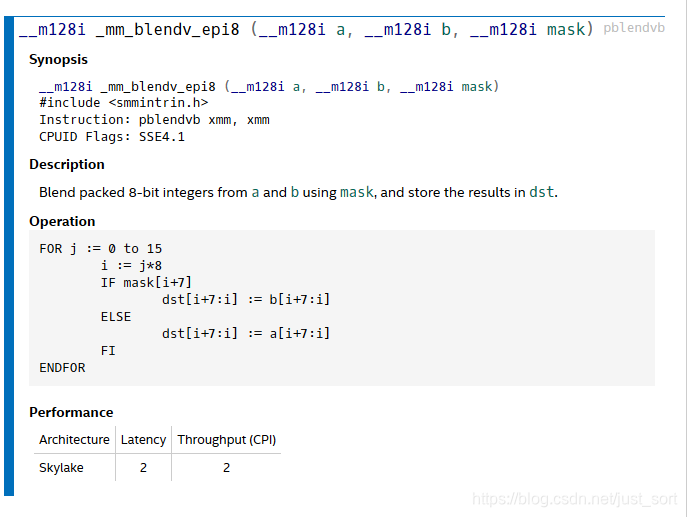
_mm_blendv_epi8 指令

另外一种是利用_mm_or_si128指令：

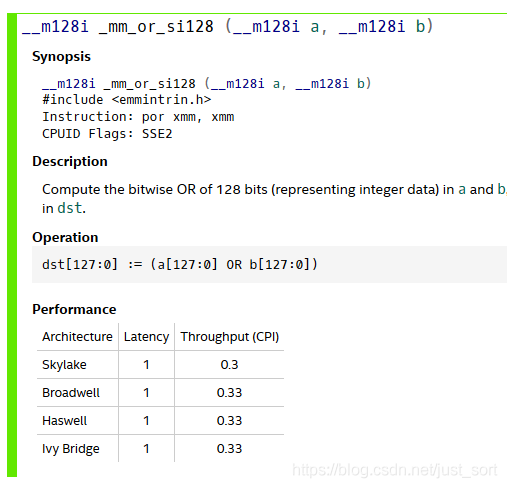
_mm_or_si128 指令

考虑到简洁性，这段代码中直接利用了第二种方式实现。

_mm_storeu_si128把处理的结果写入到目标内存中，注意，这里会多写了4个字节的内存数据（128 - 12 * 8），但是我们后面又会把他们重新覆盖掉，但是有一点要注意，就是如果是最后一行数据，在某些情况下超出的这个几个字节就已经不属于你这个进程该管理的范围了， 这个时候就会出现OOM错误，因此一种简单的方式就是在宽度方向上的循环终止条件设置为： X < Width - 12；这样剩余的像素用普通的算法处理即可避免这种问题出现。

10. 总结¶

我们来看一下使用上面介绍的这些优化获得的结果汇总。

分辨率	优化	循环次数	速度
4032x3024	原始实现	100	34.87ms
4032x3024	第一版优化	100	23.10ms
4032x3024	OpenCV 自带函数	100	18.23ms
4032x3024	第二版优化	100	17.76ms
4032x3024	第三版(SSE)优化	100	10.54ms

我添加了OpenCV自带函数的测试，可以经过我们的优化，RGB转Gray算法的速度已经超越了OpenCV自带函数的速度，注意我的OpenCV版本为：OpenCV 3.4.0。

所以指令集优化确实是有用并且值得研究的，后面将持续输出，为大家带来更多的优化实例和优化技巧。

11. 参考¶

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

本文总阅读量次