1. 前言¶

继续优化技术的探索，今天以一个 $3\times 3$ 的Sobel算子进行边缘检测的算法为例来看看如何使用SSE指令集对其进行优化。

2. 原理介绍¶

众所周知，在传统的图像边缘检测算法中，最常用的一种算法是利用Sobel算子完成的。Sobel算子一共有 $2$ 个，一个是检测水平边缘的算子，另一个是检测垂直边缘的算子。

Sobel算子的优点是可以利用快速卷积函数，简单有效，且对领域像素位置的影响做了加权，可以降低边缘模糊程度，有较好效果。然而Sobel算子并没有基于图像的灰度信息进行处理，所以在提取图像边缘信息的时候可能不会让人视觉满意。

我们来看一下怎么构造Sobel算子？

Sobel算子是在一个坐标轴的方向进行非归一化的高斯平滑，在另外一个坐标轴方向做一个差分， $kszie\times ksize$ 大小的Sobel算子是由平滑算子和差分算子全卷积得到，其中 $ksize$ 代表Sobel算子的半径，必须为奇数。

对于窗口大小为 $ksize$ 的非归一化Sobel平滑算子等于 $ksize-1$ 阶的二项式展开式的系数，而Sobel平滑算子等于 $ksize-2$ 阶的二项式展开式的系数两侧补 $0$ ，然后向前差分。

在这个例子中：我们要构造一个 $3$ 阶的Sobel非归一化的Sobel平滑算子和Sobel差分算子：

Sobel平滑算子：取二项式的阶数为 $n=2$ ，然后计算展开式系数为， $[C_2^0, C_2^1, C_2^2]$ 也即是 $[1, 2, 1]$ ，这就是 $3$ 阶的非归一化的Sobel平滑算子。

Sobel差分算子：取二项式的阶数为 $n=3-2=1$ ，然后计算二项展开式的系数，即为： $[C_1^0, C_1^1]$ ，两侧补 $0$ 并且前向差分得到 $[1, 0,-1]$ ，第 $4$ 项差分后可以直接删除。

Sobel算子：将 $3$ 阶的Sobel平滑算子和Sobel差分算子进行全卷积，即可得到 $3\times 3$ 的Sobel算子。

其中 $x$ 方向的Sobel算子为：

$soble_x=\begin{bmatrix} 1 \\2\\1 \end{bmatrix} * \begin{bmatrix} 1 & 0 &-1\end{bmatrix}=\begin{bmatrix} 1 &0&-1\\2&0&-2\\1&0&-1 \end{bmatrix}$

而 $y$ 方向的Sobel算子为：

$sobel_y=\begin{bmatrix} 1 &0&-1 \end{bmatrix}*\begin{bmatrix} 1 \\2\\1 \end{bmatrix}=\begin{bmatrix} 1&2&1\\0&0&0\\-1&-2&-1 \end{bmatrix}$

3. 原始实现¶

我们先放出针对 $3\times 3$ 的Sobel算子的原始实现代码，如下所示：

inline unsigned char IM_ClampToByte(int Value)
{
    if (Value < 0)
        return 0;
    else if (Value > 255)
        return 255;
    else
        return (unsigned char)Value;
    //return ((Value | ((signed int)(255 - Value) >> 31)) & ~((signed int)Value >> 31));
}

void Sobel_FLOAT(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    int Channel = Stride / Width;
    unsigned char *RowCopy = (unsigned char*)malloc((Width + 2) * 3 * Channel);
    unsigned char *First = RowCopy;
    unsigned char *Second = RowCopy + (Width + 2) * Channel;
    unsigned char *Third = RowCopy + (Width + 2) * 2 * Channel;
    //拷贝第二行数据，边界值填充
    memcpy(Second, Src, Channel);
    memcpy(Second + Channel, Src, Width*Channel);
    memcpy(Second + (Width + 1)*Channel, Src + (Width - 1)*Channel, Channel);
    //第一行和第二行一样
    memcpy(First, Second, (Width + 2) * Channel);
    //拷贝第三行数据，边界值填充
    memcpy(Third, Src + Stride, Channel);
    memcpy(Third + Channel, Src + Stride, Width * Channel);
    memcpy(Third + (Width + 1) * Channel, Src + Stride + (Width - 1) * Channel, Channel);

    for (int Y = 0; Y < Height; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Stride;
        if (Y != 0) {
            unsigned char *Temp = First;
            First = Second;
            Second = Third;
            Third = Temp;
        }
        if (Y == Height - 1) {
            memcpy(Third, Second, (Width + 2) * Channel);
        }
        else {
            memcpy(Third, Src + (Y + 1) * Stride, Channel);
            memcpy(Third + Channel, Src + (Y + 1) * Stride, Width * Channel);                            //    由于备份了前面一行的数据，这里即使Src和Dest相同也是没有问题的
            memcpy(Third + (Width + 1) * Channel, Src + (Y + 1) * Stride + (Width - 1) * Channel, Channel);
        }
        if (Channel == 1) {
            for (int X = 0; X < Width; X++)
            {
                int GX = First[X] - First[X + 2] + (Second[X] - Second[X + 2]) * 2 + Third[X] - Third[X + 2];
                int GY = First[X] + First[X + 2] + (First[X + 1] - Third[X + 1]) * 2 - Third[X] - Third[X + 2];
                LinePD[X] = IM_ClampToByte(sqrtf(GX * GX + GY * GY + 0.0F));
            }
        }
        else
        {
            for (int X = 0; X < Width * 3; X++)
            {
                int GX = First[X] - First[X + 6] + (Second[X] - Second[X + 6]) * 2 + Third[X] - Third[X + 6];
                int GY = First[X] + First[X + 6] + (First[X + 3] - Third[X + 3]) * 2 - Third[X] - Third[X + 6];
                LinePD[X] = IM_ClampToByte(sqrtf(GX * GX + GY * GY + 0.0F));
            }
        }
    }
    free(RowCopy);
}

这段代码有两个主要特点，一是它支持In-Place操作，也即是说Src和Dest可以是同一块内存；二是，这个代码考虑了边缘Padding，边界处理在图像处理中是比较重要的。

速度测试结果如下：

分辨率	算法优化	循环次数	速度
4032x3024	普通实现	1000	126.54ms

4. Sobel边缘检测算法优化第一版¶

一个比较显然的优化方法是把上述代码中的IM_ClampToByte(sqrtf(GX * GX + GY * GY + 0.0F))利用查表法的技巧来优化，简单改成下面的版本，避免了浮点数运算。注意为什么表的长度最多是65026？因为255*255=65025，所以开方之后最大值为255，也即是像素的最大表示范围，所以超过65025其实都是无效的。

void Sobel_INT(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    int Channel = Stride / Width;
    unsigned char *RowCopy = (unsigned char*)malloc((Width + 2) * 3 * Channel);
    unsigned char *First = RowCopy;
    unsigned char *Second = RowCopy + (Width + 2) * Channel;
    unsigned char *Third = RowCopy + (Width + 2) * 2 * Channel;
    //拷贝第二行数据，边界值填充
    memcpy(Second, Src, Channel);
    memcpy(Second + Channel, Src, Width*Channel);
    memcpy(Second + (Width + 1)*Channel, Src + (Width - 1)*Channel, Channel);
    //第一行和第二行一样
    memcpy(First, Second, (Width + 2) * Channel);
    //拷贝第三行数据，边界值填充
    memcpy(Third, Src + Stride, Channel);
    memcpy(Third + Channel, Src + Stride, Width * Channel);
    memcpy(Third + (Width + 1) * Channel, Src + Stride + (Width - 1) * Channel, Channel);

    unsigned char Table[65026];
    for (int Y = 0; Y < 65026; Y++) Table[Y] = (sqrtf(Y + 0.0f) + 0.5f);
    for (int Y = 0; Y < Height; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Stride;
        if (Y != 0) {
            unsigned char *Temp = First;
            First = Second;
            Second = Third;
            Third = Temp;
        }
        if (Y == Height - 1) {
            memcpy(Third, Second, (Width + 2) * Channel);
        }
        else {
            memcpy(Third, Src + (Y + 1) * Stride, Channel);
            memcpy(Third + Channel, Src + (Y + 1) * Stride, Width * Channel);                            //    由于备份了前面一行的数据，这里即使Src和Dest相同也是没有问题的
            memcpy(Third + (Width + 1) * Channel, Src + (Y + 1) * Stride + (Width - 1) * Channel, Channel);
        }
        if (Channel == 1) {
            for (int X = 0; X < Width; X++)
            {
                int GX = First[X] - First[X + 2] + (Second[X] - Second[X + 2]) * 2 + Third[X] - Third[X + 2];
                int GY = First[X] + First[X + 2] + (First[X + 1] - Third[X + 1]) * 2 - Third[X] - Third[X + 2];
                LinePD[X] = Table[min(GX * GX + GY * GY, 65025)];
            }
        }
        else
        {
            for (int X = 0; X < Width * 3; X++)
            {
                int GX = First[X] - First[X + 6] + (Second[X] - Second[X + 6]) * 2 + Third[X] - Third[X + 6];
                int GY = First[X] + First[X + 6] + (First[X + 3] - Third[X + 3]) * 2 - Third[X] - Third[X + 6];
                LinePD[X] = Table[min(GX * GX + GY * GY, 65025)];
            }
        }
    }
    free(RowCopy);
}

分辨率	算法优化	循环次数	速度
4032x3024	普通实现	1000	126.54ms
4032x3024	Float->INT+查表法	1000	81.62ms

5. Sobel边缘检测算法优化第二版¶

再第一版优化的代码基础上，我们来考虑一下使用SSE来进行算法优化。从代码中可以看到对于灰度图的优化是没有必要的，因为在计算的时候当前像素只和另外两个像素相关：

当Channel=1的时候，当前像素只和另外两个像素相关

这里面涉及到了8个不同的像素，考虑到计算的特性和数据的范围，在内部计算时这个int可以用short代替，也就是先把加载的字节型数据转换成short类型，这样就可以用8个SSE变量记录8个连续的像素值，每个像素值用16位的数据来表达，这里可以使用_mm_loadl_epi64配合_mm_unpacklo_epi8来实现，其中_mm_loadl_epi64指令实现的功能如下：

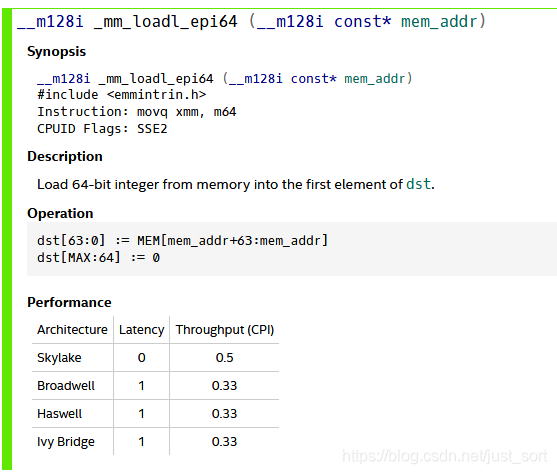
_mm_loadl_epi64 指令

而_mm_unpacklo_epi8指令实现的功能如下：

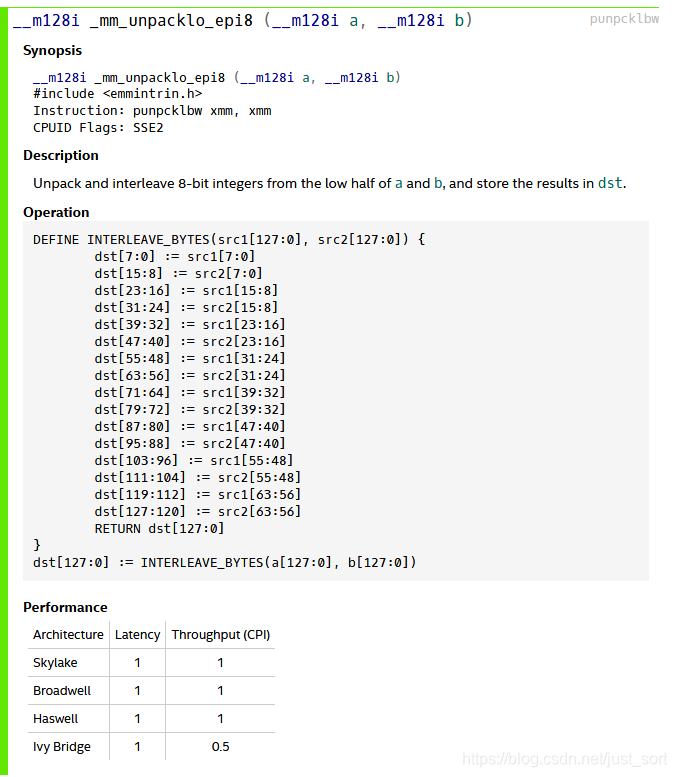
_mm_unpacklo_epi8 指令

因此，这部分的代码实现如下：

__m128i FirstP0 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(First + X)), Zero);
__m128i FirstP1 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(First + X + 3)), Zero);
__m128i FirstP2 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(First + X + 6)), Zero);

__m128i SecondP0 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(Second + X)), Zero);
__m128i SecondP2 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(Second + X + 6)), Zero);

__m128i ThirdP0 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(Third + X)), Zero);
__m128i ThirdP1 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(Third + X + 3)), Zero);
__m128i ThirdP2 = _mm_unpacklo_epi8(_mm_loadl_epi64((__m128i *)(Third + X + 6)), Zero);

接下来我们开始对GX和GY进行计算：

__m128i GX16 = _mm_abs_epi16(_mm_add_epi16(_mm_add_epi16(_mm_sub_epi16(FirstP0, FirstP2), _mm_slli_epi16(_mm_sub_epi16(SecondP0, SecondP2), 1)), _mm_sub_epi16(ThirdP0, ThirdP2)));
__m128i GY16 = _mm_abs_epi16(_mm_sub_epi16(_mm_add_epi16(_mm_add_epi16(FirstP0, FirstP2), _mm_slli_epi16(_mm_sub_epi16(FirstP1, ThirdP1), 1)), _mm_add_epi16(ThirdP0, ThirdP2)));

这个时候的GX16和GY16里保存的是8个16位的中间结果，由于SSE只提供了浮点数的sqrt操作，我们必须将它们转换为浮点数，那么这个转换的第一步就必须是先将它们转换为int的整形数，这样，就必须一个拆成2个，即：

__m128i GX32L = _mm_unpacklo_epi16(GX16, Zero);
__m128i GX32H = _mm_unpackhi_epi16(GX16, Zero);
__m128i GY32L = _mm_unpacklo_epi16(GY16, Zero);
__m128i GY32H = _mm_unpackhi_epi16(GY16, Zero);

接下来分别对高位低位进行平方运算：

__m128i ResultL = _mm_cvtps_epi32(_mm_sqrt_ps(_mm_cvtepi32_ps(_mm_add_epi32(_mm_mullo_epi32(GX32L, GX32L), _mm_mullo_epi32(GY32L, GY32L)))));
__m128i ResultH = _mm_cvtps_epi32(_mm_sqrt_ps(_mm_cvtepi32_ps(_mm_add_epi32(_mm_mullo_epi32(GX32H, GX32H), _mm_mullo_epi32(GY32H, GY32H)))));

最后一步，得到8个uchar型的结果，这个结果有要转换为字节类型的，并且这些数据有可能会超出字节所能表达的范围，所以就需要用到SSE的抗饱和向下打包指令了：

_mm_storel_epi64((__m128i *)(LinePD + X), _mm_packus_epi16(_mm_packus_epi32(ResultL, ResultH), Zero));

OK，现在来测一把速度：

分辨率	算法优化	循环次数	速度
4032x3024	普通实现	1000	126.54ms
4032x3024	Float->INT+查表法	1000	81.62ms
4032x3024	SSE优化版本1	1000	34.95ms

在上面的代码中还要额外注意一点，通常，我们都是对像素的字节数据进行向上扩展，他们都是正数，所以用unpack之类的配合zero把高8位或高16位的数据填充为0就可以了，但是在本例中，GX16或者GY16很有可能是负数，而负数的最高位是符号位，如果都填充为0，则变为正数了，明显改变原始的数据了，所以得到了错误的结果。

那么我们是如何解决这个问题的呢？

对于这个例子，因为后面只有一个平方操作，因此对GX先取绝对值是不会改变计算的结果的，这样就不会出现负的数据了，修改之后，果然结果正确。

6. Sobel边缘检测算法优化第三版¶

从ImageShop博主那里继续学到了另外一种优化方法，我们观察一下最后计算 $GX*GX+GY*GY$ 的过程，我们知道，SSE3提供了一个_mm_madd_epi16指令，其作用是：

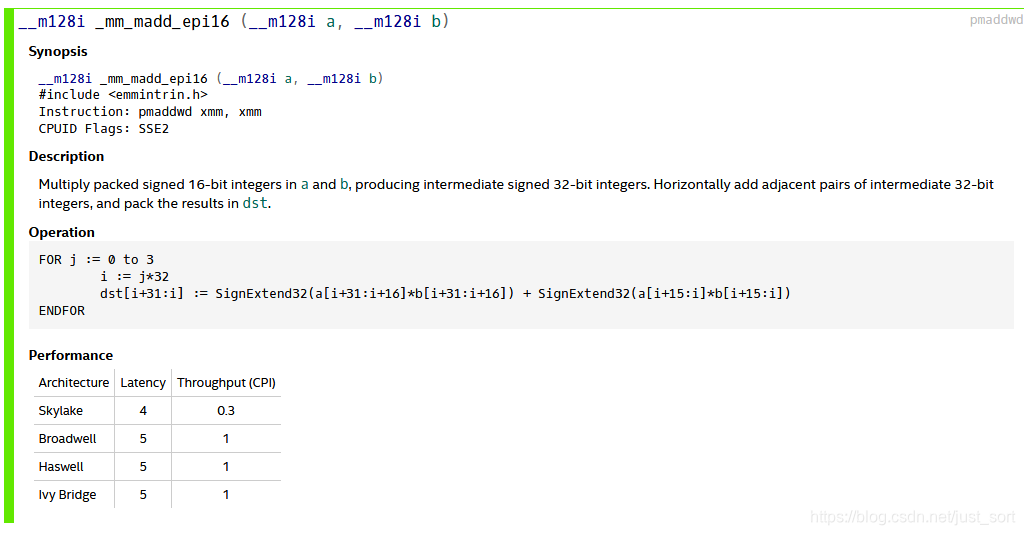_mm_madd_epi16 指令如果我们可以把GX和GY的数据拼接成另外两个数据：

GXYL = GX0 GY0 GX1 GY1 GX2 GY2 GX3 GY3

GXYH = GX4 GY4 GX5 GY5 GX6 GY6 GX7 GY7

那么直接调用_mm_madd_epi16(GXYL，GXYL)和_mm_madd_epi16(GXYH, GXYH)不就能得到和之前一样的结果了？并且这个拼接可以使用下面的代码实现：

__m128i GXYL = _mm_unpacklo_epi16(GX16, GY16);
__m128i GXYH = _mm_unpackhi_epi16(GX16, GY16);

这样上一个版本中的10条SIMD指令就变成了4条，代码更加简洁并且速度也更快了。

来测一把速度：

分辨率	算法优化	循环次数	速度
4032x3024	普通实现	1000	126.54ms
4032x3024	Float->INT+查表法	1000	81.62ms
4032x3024	SSE优化版本1	1000	34.95ms
4032x3024	SSE优化版本2	1000	28.87ms

7. Sobel边缘检测算法优化第四版¶

在SSE中每次只能处理8个结果，自然使用AVX指令集来完成单次16个像素的处理，AVX版本的代码实现如下：

unsigned char *RowCopy;
unsigned char *First;
unsigned char *Second;
unsigned char *Third;
int Channel, Block, BlockSize;
void _Sobel(unsigned char* Src, const int32_t Width, const int32_t Height, const int32_t start_row, const int32_t thread_stride, const int32_t Stride, unsigned char* Dest) {
    for (int Y = start_row; Y < start_row + thread_stride; Y++) {
        unsigned char *LinePS = Src + Y * Stride;
        unsigned char *LinePD = Dest + Y * Stride;
        if (Y != 0) {
            unsigned char *Temp = First;
            First = Second;
            Second = Third;
            Third = Temp;
        }
        if (Y == Height - 1) {
            memcpy(Third, Second, (Width + 2) * Channel);
        }
        else {
            memcpy(Third, Src + (Y + 1) * Stride, Channel);
            memcpy(Third + Channel, Src + (Y + 1) * Stride, Width * Channel);                            //    由于备份了前面一行的数据，这里即使Src和Dest相同也是没有问题的
            memcpy(Third + (Width + 1) * Channel, Src + (Y + 1) * Stride + (Width - 1) * Channel, Channel);
        }
        if (Channel == 1) {
            for (int X = 0; X < Width; X++)
            {
                int GX = First[X] - First[X + 2] + (Second[X] - Second[X + 2]) * 2 + Third[X] - Third[X + 2];
                int GY = First[X] + First[X + 2] + (First[X + 1] - Third[X + 1]) * 2 - Third[X] - Third[X + 2];
                //LinePD[X] = Table[min(GX * GX + GY * GY, 65025)];
            }
        }
        else
        {
            __m256i Zero = _mm256_setzero_si256();
            for (int X = 0; X < Block * BlockSize; X += BlockSize)
            {
                __m256i FirstP0 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(First + X)));
                __m256i FirstP1 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(First + X + 3)));
                __m256i FirstP2 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(First + X + 6)));

                __m256i SecondP0 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(Second + X)));
                __m256i SecondP2 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(Second + X + 6)));

                __m256i ThirdP0 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(Third + X)));
                __m256i ThirdP1 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(Third + X + 3)));
                __m256i ThirdP2 = _mm256_cvtepu8_epi16(_mm_loadu_si128((const __m128i*)(Third + X + 6)));

                //GX0   GX1     GX2    GX3    GX4    GX5    GX6    GX7     GX8   GX9     GX10    GX11    GX12    GX13    GX14    GX15
                __m256i GX16 = _mm256_abs_epi16(_mm256_adds_epi16(_mm256_adds_epi16(_mm256_subs_epi16(FirstP0, FirstP2), _mm256_slli_epi16(_mm256_subs_epi16(SecondP0, SecondP2), 1)), _mm256_subs_epi16(ThirdP0, ThirdP2)));
                //GY0   GY1     GY2    GY3    GY4    GY5    GY6    GY7     GY8   GY9     GY10    GY11    GY12    GY13    GY14    GY15
                __m256i GY16 = _mm256_abs_epi16(_mm256_subs_epi16(_mm256_adds_epi16(_mm256_adds_epi16(FirstP0, FirstP2), _mm256_slli_epi16(_mm256_subs_epi16(FirstP1, ThirdP1), 1)), _mm256_adds_epi16(ThirdP0, ThirdP2)));
                //GX0　　GY0　　GX1　　GY1　　GX2　　GY2　　GX3　　GY3    GX4    GY4     GX5     GY5      GX6     GY6     GX7     GY7
                __m256i GXYL = _mm256_unpacklo_epi16(GX16, GY16);
                //GX8　　GY8　　GX9　　GY9　　GX10　GY10　　GX11　GY11    GX12   GY12    GX13    GY13     GX14    GY14    GX15    GY15     
                __m256i GXYH = _mm256_unpackhi_epi16(GX16, GY16);


                __m256i ResultL = _mm256_cvtps_epi32(_mm256_sqrt_ps(_mm256_cvtepi32_ps(_mm256_madd_epi16(GXYL, GXYL))));
                __m256i ResultH = _mm256_cvtps_epi32(_mm256_sqrt_ps(_mm256_cvtepi32_ps(_mm256_madd_epi16(GXYH, GXYH))));

                __m256i Result = _mm256_packus_epi16(_mm256_packus_epi32(ResultL, ResultH), Zero);

                __m128i Ans = _mm256_castsi256_si128(Result);
                _mm_storeu_si128((__m128i *)(LinePD + X), Ans);
            }

            for (int X = Block * BlockSize; X < Width * 3; X++)
            {
                int GX = First[X] - First[X + 6] + (Second[X] - Second[X + 6]) * 2 + Third[X] - Third[X + 6];
                int GY = First[X] + First[X + 6] + (First[X + 3] - Third[X + 3]) * 2 - Third[X] - Third[X + 6];
                LinePD[X] = IM_ClampToByte(sqrtf(GX * GX + GY * GY + 0.0F));
            }
        }
    }
}

void Sobel_AVX1(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    Channel = Stride / Width;
    RowCopy = (unsigned char*)malloc((Width + 2) * 3 * Channel);
    First = RowCopy;
    Second = RowCopy + (Width + 2) * Channel;
    Third = RowCopy + (Width + 2) * 2 * Channel;
    //拷贝第二行数据，边界值填充
    memcpy(Second, Src, Channel);
    memcpy(Second + Channel, Src, Width*Channel);
    memcpy(Second + (Width + 1)*Channel, Src + (Width - 1)*Channel, Channel);
    //第一行和第二行一样
    memcpy(First, Second, (Width + 2) * Channel);
    //拷贝第三行数据，边界值填充
    memcpy(Third, Src + Stride, Channel);
    memcpy(Third + Channel, Src + Stride, Width * Channel);
    memcpy(Third + (Width + 1) * Channel, Src + Stride + (Width - 1) * Channel, Channel);

    BlockSize = 16, Block = (Width * Channel) / BlockSize;

    _Sobel(Src, Width, Height, 0, Height, Stride, Dest);

    free(RowCopy);
}

测试一把速度：

分辨率	算法优化	循环次数	速度
4032x3024	普通实现	1000	126.54ms
4032x3024	Float->INT+查表法	1000	81.62ms
4032x3024	SSE优化版本1	1000	34.95ms
4032x3024	SSE优化版本2	1000	28.87ms
4032x3024	AVX2优化	1000	15.42ms

8. Sobel边缘检测算法优化第五版¶

和上回的推文一样，我们结合一下std::async进行异步并行优化，代码如下：

void Sobel_AVX2(unsigned char *Src, unsigned char *Dest, int Width, int Height, int Stride) {
    //INIT
    Channel = Stride / Width;
    RowCopy = (unsigned char*)malloc((Width + 2) * 3 * Channel);
    First = RowCopy;
    Second = RowCopy + (Width + 2) * Channel;
    Third = RowCopy + (Width + 2) * 2 * Channel;
    //拷贝第二行数据，边界值填充
    memcpy(Second, Src, Channel);
    memcpy(Second + Channel, Src, Width*Channel);
    memcpy(Second + (Width + 1)*Channel, Src + (Width - 1)*Channel, Channel);
    //第一行和第二行一样
    memcpy(First, Second, (Width + 2) * Channel);
    //拷贝第三行数据，边界值填充
    memcpy(Third, Src + Stride, Channel);
    memcpy(Third + Channel, Src + Stride, Width * Channel);
    memcpy(Third + (Width + 1) * Channel, Src + Stride + (Width - 1) * Channel, Channel);

    BlockSize = 16, Block = (Width * Channel) / BlockSize;

    //Run
    const int32_t hw_concur = std::min(Height >> 4, static_cast<int32_t>(std::thread::hardware_concurrency()));
    std::vector<std::future<void>> fut(hw_concur);
    const int thread_stride = (Height - 1) / hw_concur + 1;
    int i = 0, start = 0;
    for (; i < std::min(Height, hw_concur); i++, start += thread_stride)
    {
        fut[i] = std::async(std::launch::async, _Sobel, Src, Width, Height, start, thread_stride, Stride, Dest);
    }
    for (int j = 0; j < i; ++j)
        fut[j].wait();

    free(RowCopy);
}

速度测试结果如下：

分辨率	算法优化	循环次数	速度
4032x3024	普通实现	1000	126.54ms
4032x3024	Float->INT+查表法	1000	81.62ms
4032x3024	SSE优化版本1	1000	34.95ms
4032x3024	SSE优化版本2	1000	28.87ms
4032x3024	AVX2优化	1000	15.42ms
4032x3024	AVX2优化+std::async	1000	5.69ms

9. 总结¶

这一篇推文展示了如何一步步优化一个 $3\times 3$ 的Sobel边缘检测算法，从原始的126.54ms优化到了5.69ms，加速比为22倍。

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

本文总阅读量次