可能是讲得最清楚的WeightOnlyGEMM

引言¶

WeightOnly GEMM技术是在一篇NVIDIA和Microsoft合作的加速MoE推理论文中提出的。

研究动机为： - MoE模型较大，如果以FP16半精度形式，传统推理卡如T4（16GB显存）存不下完整的一个模型 - MoE的矩阵乘需要多个experts专家加载权重，进而是一个memory bound操作，而不是compute bound

对于LLM推理有什么可借鉴的地方？¶

LLM推理跟训练不太一样，因为是自回归解码，取的是前一个step的token进行矩阵乘计算。

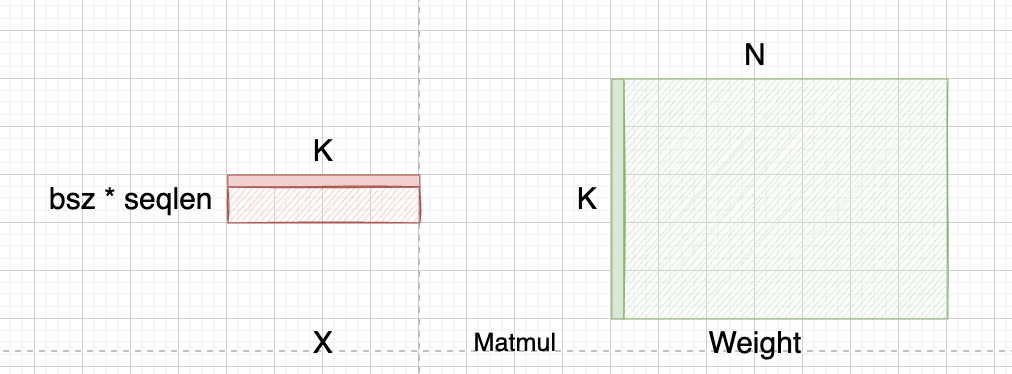
我们还是以常规的矩阵乘标记为例：

$[M, K] \odot [K, N] -> [M, N]$

在LLM矩阵乘里，M维度是 batch_size * seq_len，正如前面所提到自回归解码的特性，这里的seq_len大小为1。这么看下来，显然Weight的读取量要比输入X要大的多，计算量相对较少，进而是一个MemoryBound操作。

而更极端一点，追求时延场景下，BatchSize = 1，那么M就等于1，常规的GEMM操作进一步退化成GEMV。

WeightOnly在实际操作中： - 会在Kernel里先将int8（为了快速转换，其实加了offset转换成uint8）权重反量化成FP16进行计算，这样保证了在解决MemoryBound问题同时，也有更高的精度 - WeightOnly官方基本是直接对权重AbsMax ChannelWise/GroupWise 进行量化，相较PTQ方案，省了很多校准步骤，开箱即用。（当然我认为各有优劣，后续会谈）

WeightOnly GEMM vs Naive FP16 GEMM¶

先放出NV PPT里的BenchMark:

WeightOnly降低了Weight访存量，优化MemoryBound场景
但从Kernel计算角度考虑，相较于普通GEMM，它还额外多了一步反量化的操作

从图中我们可以得到：在BatchSize较低的情况下，相较FP16 GEMM优势明显，而随着BatchSize增大，矩阵乘M增大，WeightOnlyGEMM反而出现速度劣化。

其实在我们长Sequence情况下，也是存在类似的问题（比如最开始过Encoder Prefill阶段），在衡量首Token时延的时候，需要谨慎考虑。

下面我们详细推导下WeightOnly GEMM用到的一些技术，如快速转换

Fast Integer to Float Convert¶

作者等人通过Profile发现，Kernel的瓶颈存在于反量化的操作，准确来说就是int转float的过程。常规的我们可能以为这玩意儿不就是 static_cast<float16>(int8_weight)，但是我们可以翻下官方文档：

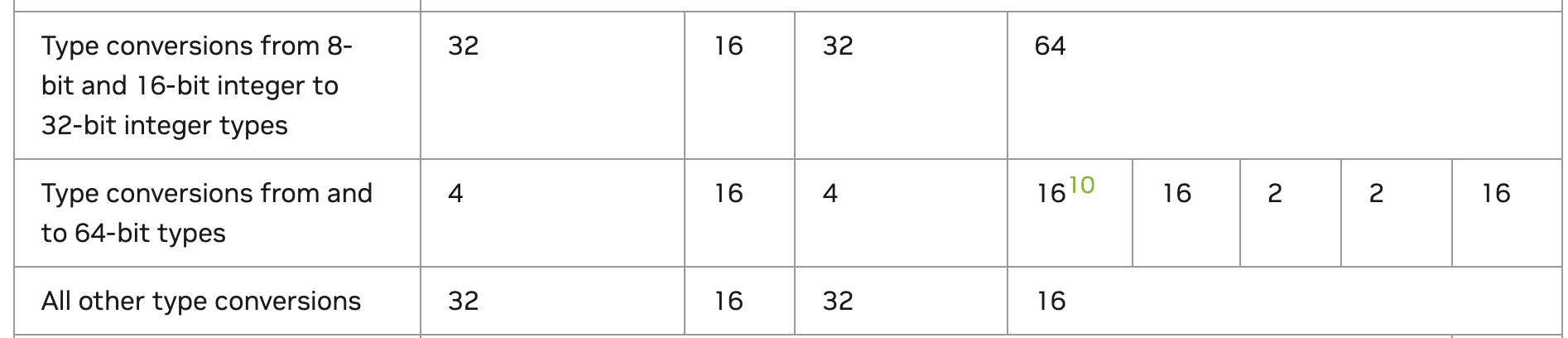
相较于GPU比较擅长的浮点运算，Type Conversion系列指令的吞吐显然就低很多了。

作者等人实现了一个优化过的Integer to Float操作后，速度明显提高不少：

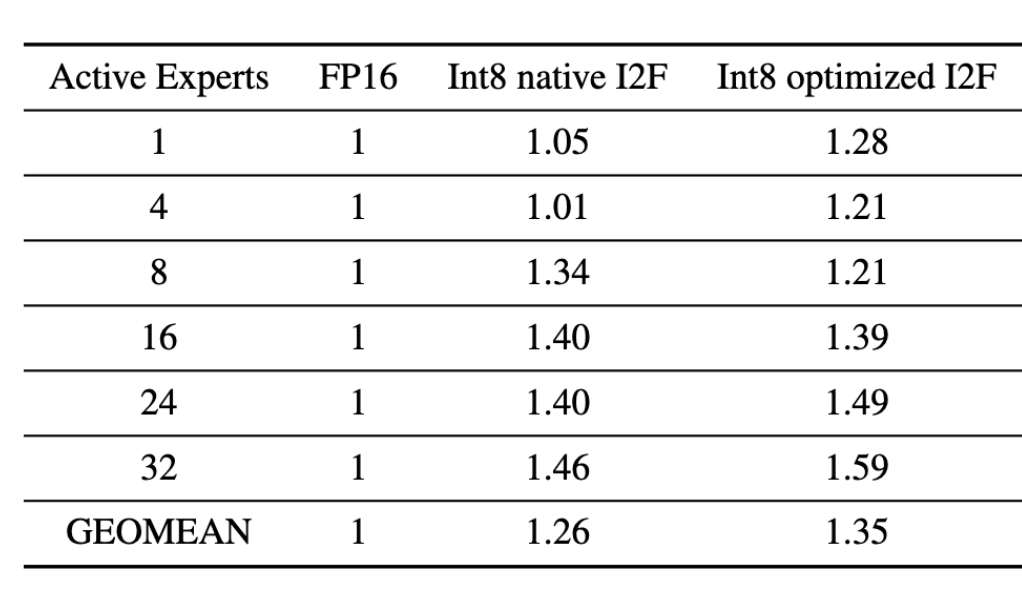
PS: 如果你单独写一个Cast Kernel去比较两个I2F操作，很大几率会是没有区别。个人经验是需要结合Kernel整体操作来看关键瓶颈是什么。

关键的代码就存在于这个Converter：

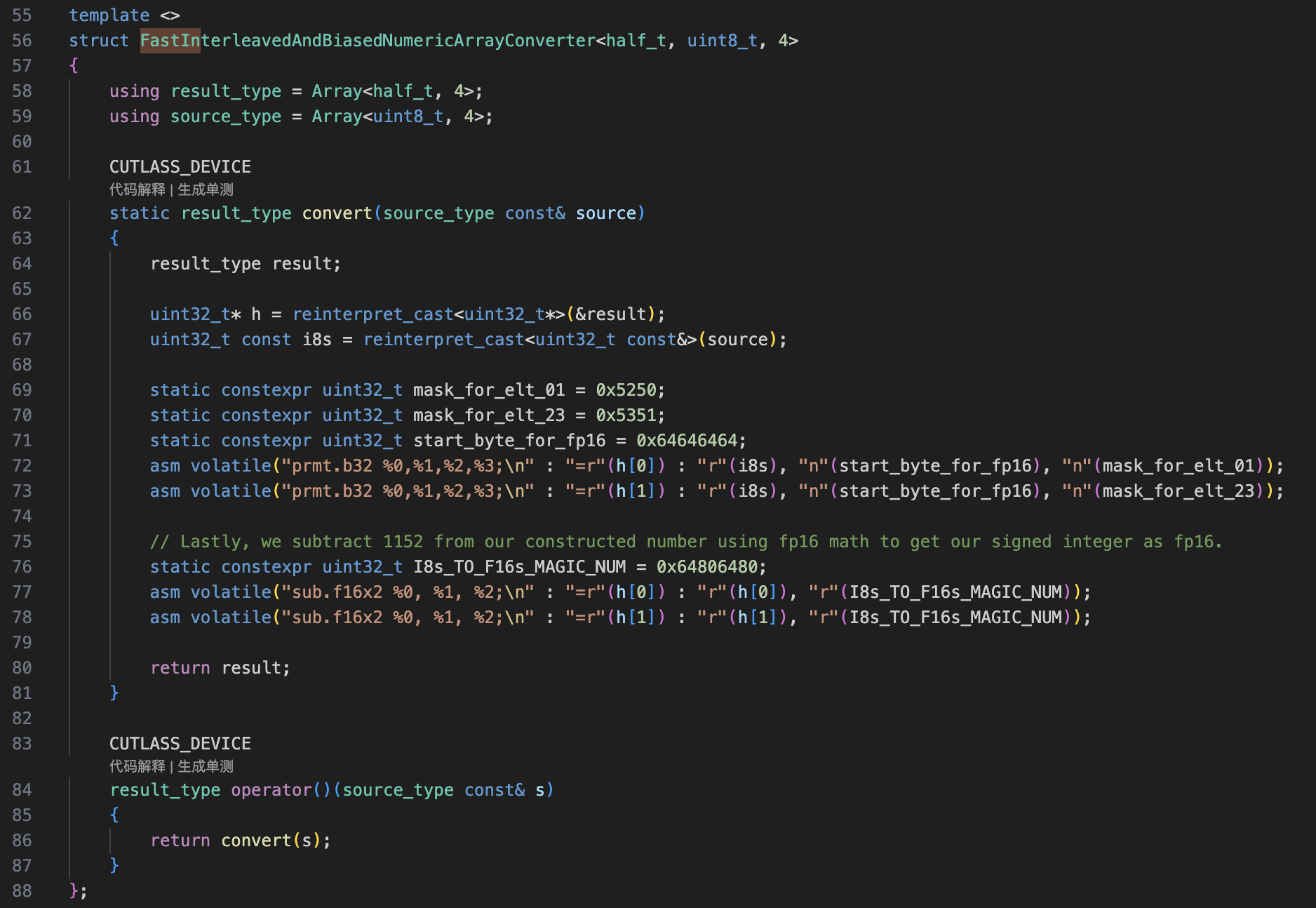
论文中提到：

对于任何 0 <= Y < 1024 的值，我们可以构造一个偏移过的FP16值 = Y + 1024，将浮点数的exponent指数位设置为1024，然后Y存储在FP16的尾数位。这个操作可以直接用一个或操作：0x6400 | Y （0x6400就是1024）完成构造

举个详细的例子：

假设你的uint8值X是3，用二进制表示：0000 0011

然后我们把0x6400拼进来，0x6400对应二进制：0110 0100

合到一块：0110 0100 0000 0011

对于fp16，符号位1个，指数位5个，尾数为：10，那么在这里对应：

符号位: 0 代表是个正数 
指数位: 11001 -> 换成十进制对应 25 
尾数位: 00 0000 0011

fp16指数位的偏移量为 2**4−1=15, 那么偏移后指数为 25 - 15 = 10.

尾数位，补上1，那么完整的就是：1.0000 0000 11

把指数乘上，相当于小数点右移10位：-> 10 0000 0011 = 1027

1024 + X = 1027 -> X = 3

看完这个例子，我们再看代码实际怎么操作的，假设我们输入的4个int8值是1, 2, 3, 4，那么对应：

asm volatile("prmt.b32 %0,%1,%2,%3;\n" : "=r"(h[0]) : "r"(i8s), "n"(start_byte_for_fp16), "n"(mask_for_elt_01));

Converter其中的一行代码是使用了PRMT指令，这个指令是先把i8s, start_byte_for_fp16的寄存器值拼到一起，然后通过mask_for_elt_01来选取，得到你想要的值。

不懂没关系，你直接看下面这张图就懂它在干啥了：

这样我们得到了：1027， 1025两个值

对于另外两个值也是类似的推导，我们再过一遍

asm volatile("prmt.b32 %0,%1,%2,%3;\n" : "=r"(h[1]) : "r"(i8s), "n"(start_byte_for_fp16), "n"(mask_for_elt_23));

这次用的是 mask_for_elt_23来选取值

这样我们得到了：1028， 1026两个值

我们完成了快速转换后，需要把多加的1024，以前预处理让int8变成unsigned int8多加的128给减去，于是还有：

static constexpr uint32_t I8s_TO_F16s_MAGIC_NUM = 0x64806480; // 就是 (1024 + 128) = 1152
asm volatile("sub.f16x2 %0, %1, %2;\n" : "=r"(h[0]) : "r"(h[0]), "r"(I8s_TO_F16s_MAGIC_NUM));
asm volatile("sub.f16x2 %0, %1, %2;\n" : "=r"(h[1]) : "r"(h[1]), "r"(I8s_TO_F16s_MAGIC_NUM));

这样就完成了我们的uint8到FP16的转换，但是细心的朋友可能观察到，我们完成转换后的元素顺序似乎变了：

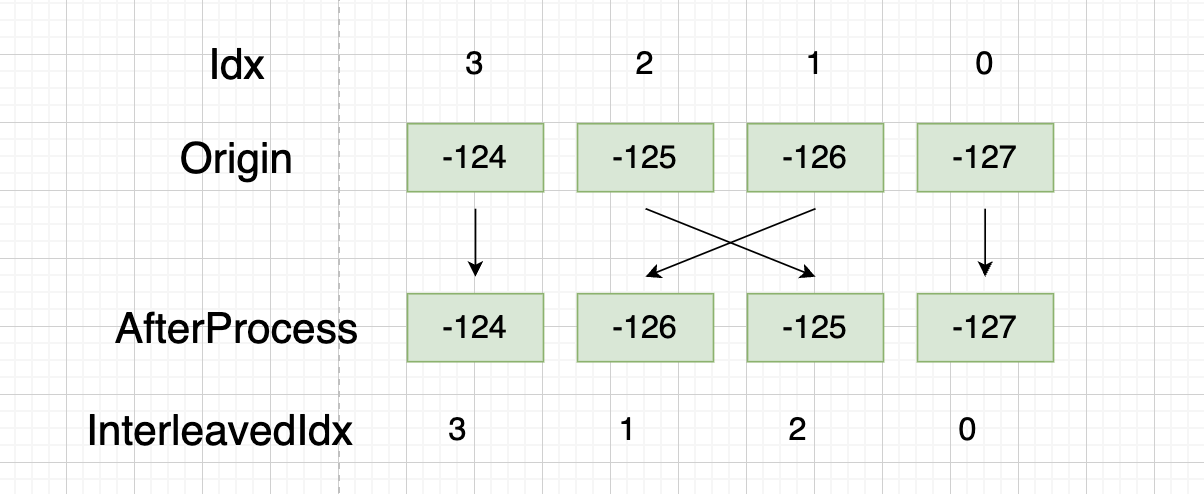
本来index为0,1,2,3变成了0,2,1,3，那么引出了我们下一个问题，为什么要交错权重？

FastInterleavedAndBiasedNumericArrayConverter 的 Interleave 交错指的就是这里

Why Interleaved ｜ WeightOnly Int4¶

对于Int8来说，本来就是不需要Interleave的，但是Int4快速转换不能使用PRMT指令，需要通过一些trick，进而需要这个交错权重的格式

下面我们来过一遍WeightOnly Int4的快速转换操作。其对应的Converter跟int8的就完全不一样了：

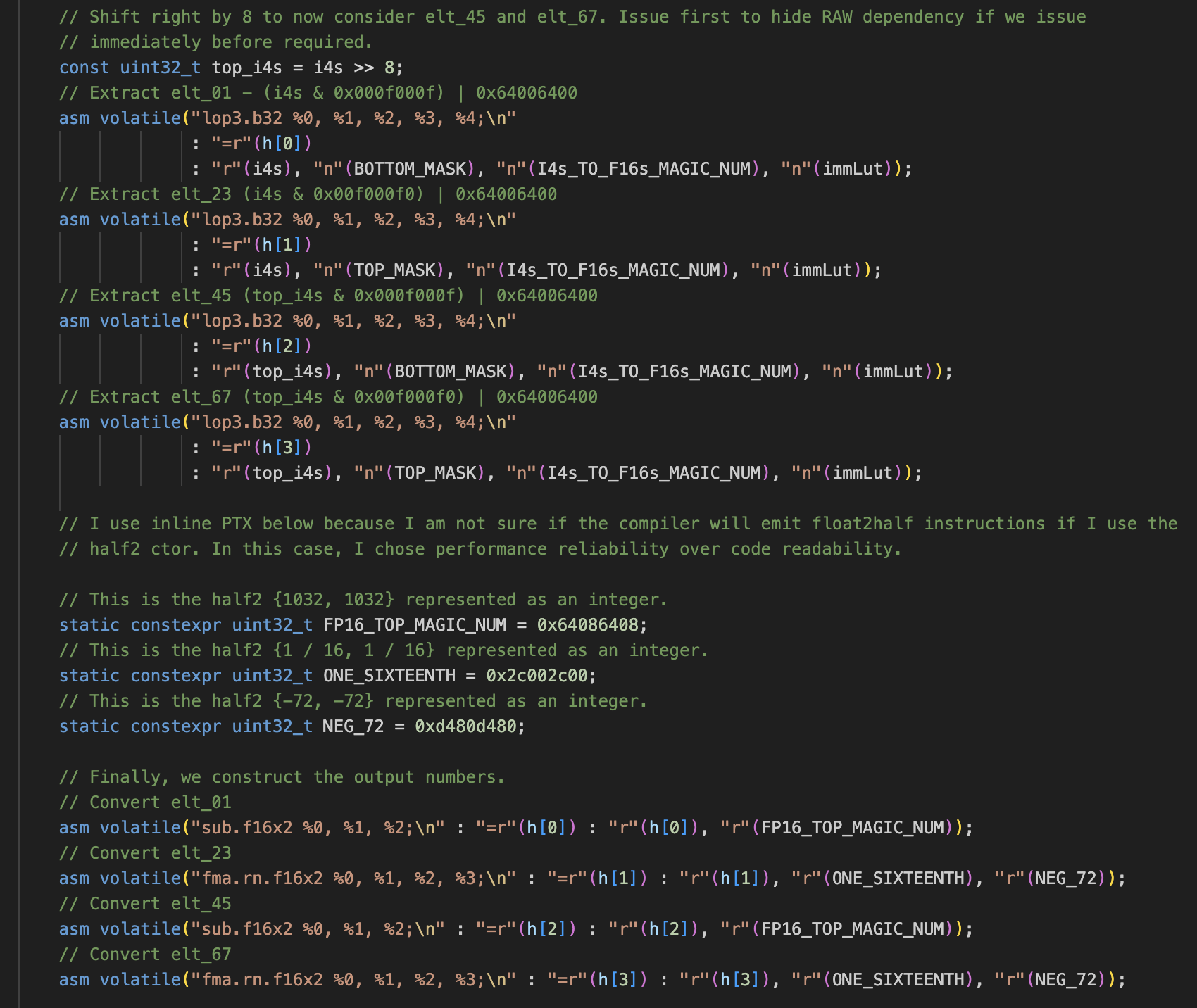
首先在权重预处理的时候，我们把int4权重Index从 0,1,2,3,4,5,6,7 -> 0,2,4,6,1,3,5,7

由于PRMT操作的是寄存器值(规定单位是Byte，即8bit），所以对于4bit无计可施。这里用的是lop3操作。

lop3是一条逻辑与+或操作，对于element0和1，我们可以用一个mask=000f000f通过与操作取到，并且和6400（就是之前我们讲的1024）或上去，就完成了+1024的操作

下面我们看element2和3:

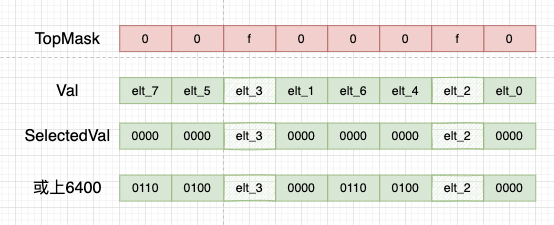
假设elt3 = 0011 elt2 = 0010 

                          elt_3                        elt_2
取到的数实际上是：    0000 0000 0011 0000       0000 0000 0010 0000
相当于左移了4位，意味着 * 16

十进制表示：                3 * 16                       2 * 16

因为多乘了16，这个后续我们也会特殊处理。接下来我们继续看element4和5:

Note: 
element4 5 6 7 的取法比较特殊

可能你会认为，这样直接用 0f00 0f00, f000 f000去取不就可以拿到了么？

但是后面我们要和6400或上，直接这么取是会冲突的（高位上冲突了，0x6400要占高位）

如图中所示冲突：

因此我们有一个额外的一个变量 top_i4s，它相当于原始int4权重做了个右移8位的操作：

这个右移操作是很巧妙的，后续取元素流程跟前面取index=0,1,2,3是完全一样的：

然后我们再假设以常规顺序排布去取，通过图例，是发现我们取不到对应元素的：

本质原因还是：

Int8下每个权重占8个bit，可以用PRMT指令去选择value放置在哪个位置

而Int4下我们选择用与+或操作取到权重，针对4个bit，这个位置已经被mask给固定了，无法选择放置在哪个位置。所以只能让他错开两位才能取到合适的结果

完成转换后，我们还需要 - 1024 - 8(无符号int4转有符号int4) = -1032

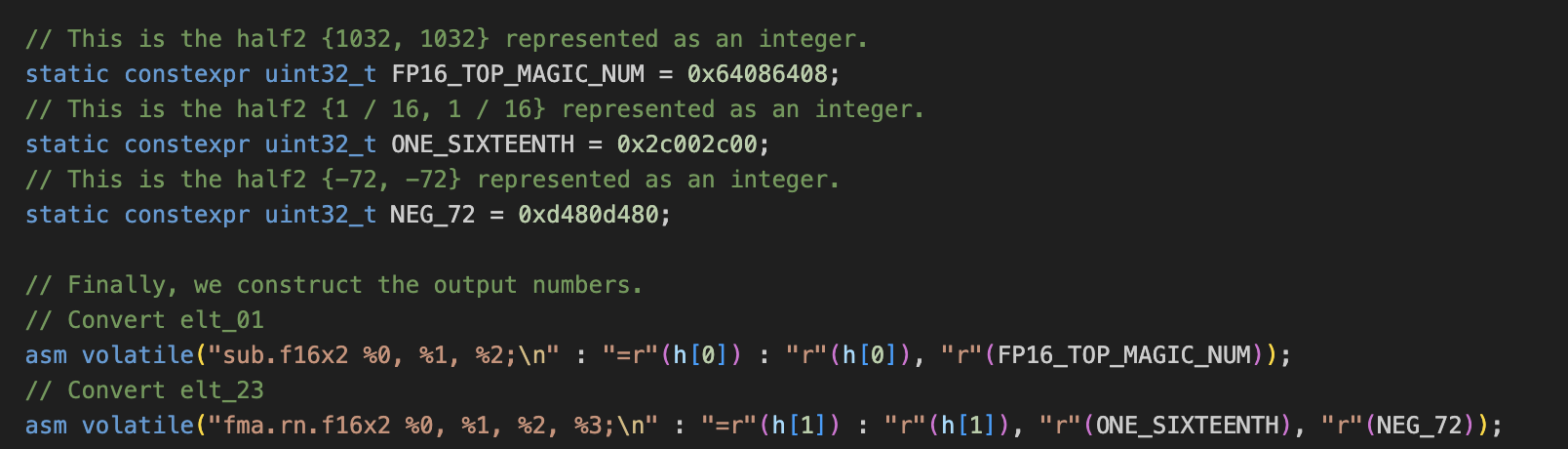
前面也提到element2 3，6 7 多乘了16，所以这几个减的时候需要考虑进去:

至此介绍完了快速int8转FP16的原理，机制，以及为什么Interleave。为了充分利用TensorCore，在权重的Layout上还有更多额外处理，下面我们一步步看

WeightOnly LayoutConvert:¶

permute_B_rows_for_mixed_gemm¶

如果你有看我先前乱谈CUTLASS GTC2020 SLIDES的使用话，那么你应该知道TensorCore对于输入排布，每个线程持有的数据，是有一定要求的。一个示例图是：

我们看黄色的B矩阵，也就是weight矩阵，他是竖着32bit，那么以FP16情况下，对应列方向，t0持有的是 row0, 1, 8, 9的数据

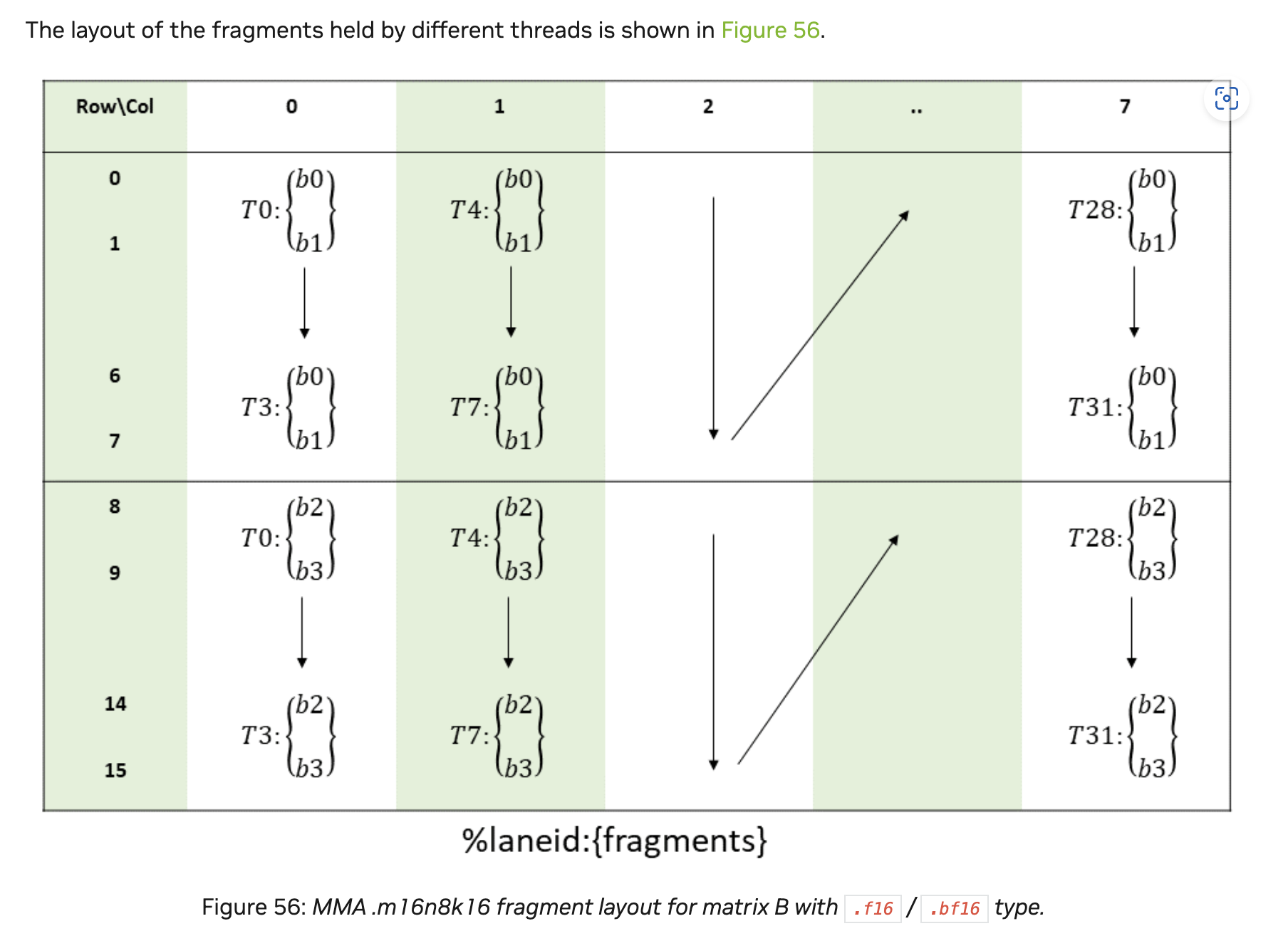
作者解释这是为了在LDSM后每个线程就直接拿到对应需要的数据，如果不做这个变换，则线程之间还需要通过一些shuffle指令拿到对应需要的数据

如果不这么做的话，你就需要像cutlass这个PR：Support for Mixed Input TensorOp

用python推过一遍index是对的，但是怎么想到用这些shuffle操作做的事真想不通。。。

subbyte_transpose¶

这个就是将权重从行优先转换成列优先：

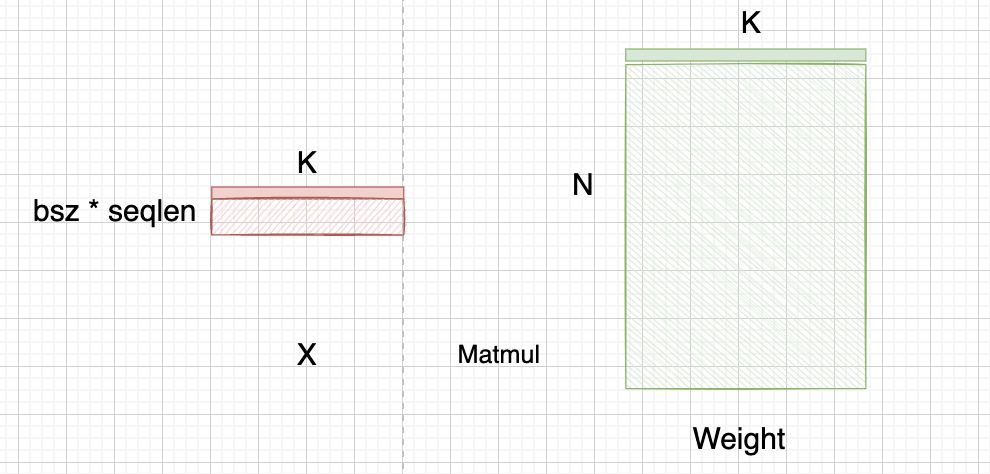
interleave_column_major_tensor¶

这个操作我个人觉得也是很关键的。首先我们复习下cutlass GEMM优化的Pipeline：

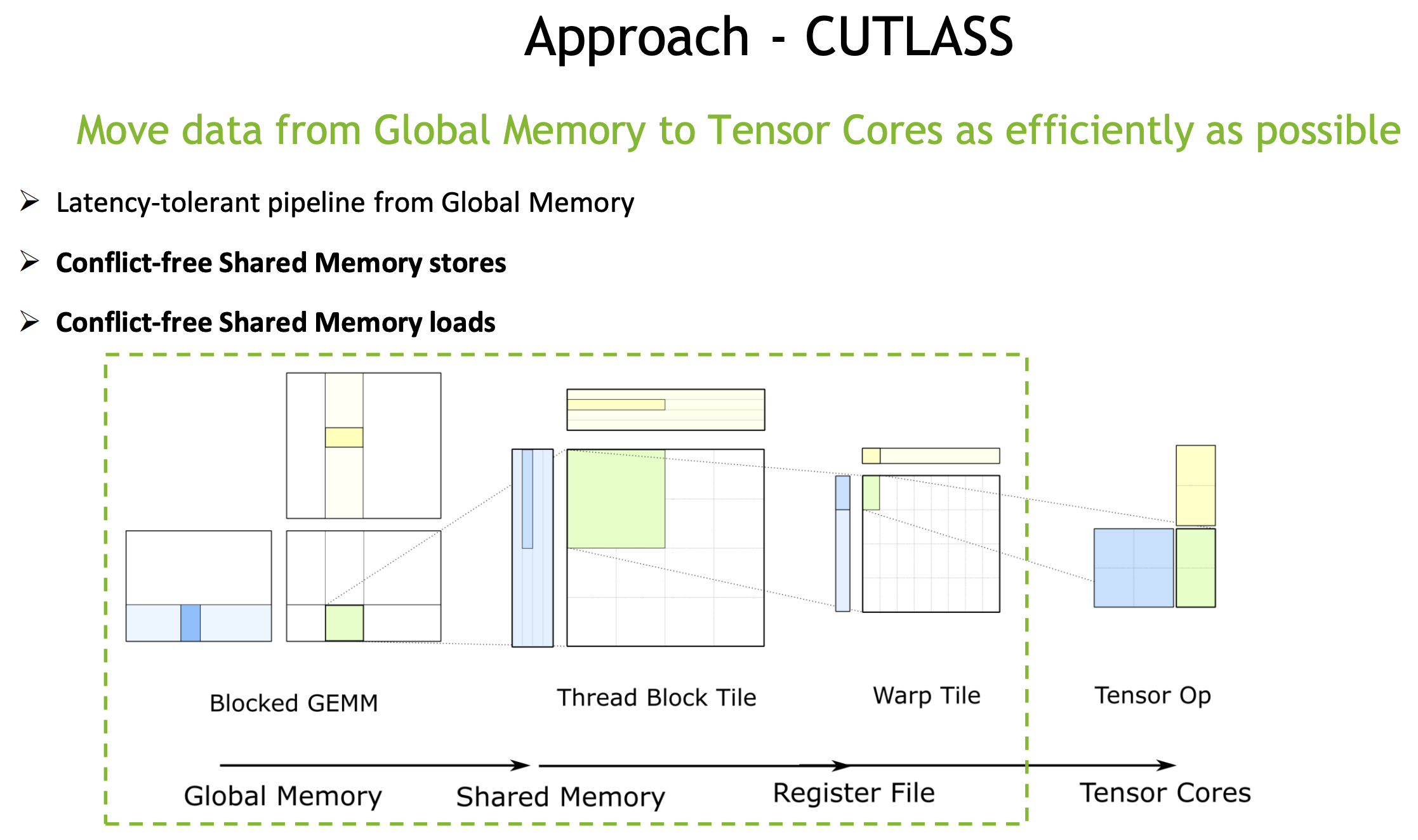
计算是对不同CUDA抽象层级Block->Warp切分子任务

数据搬运则是充分利用不同层级的存储GlobalMemory->SharedMemory->RegisterFile，避免重复读写。

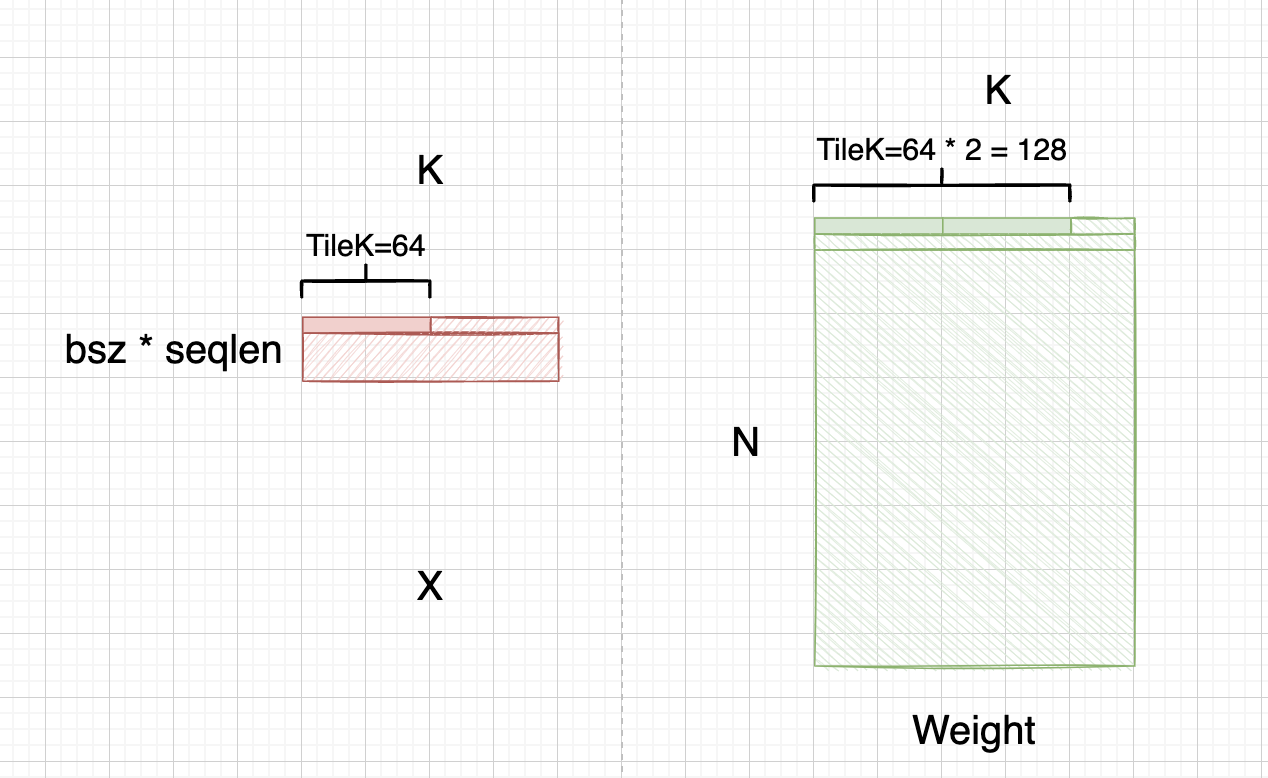
在WeightOnly GEMM实现中，其固定TileK为64

而在CUDA里，CacheLine大小为128bytes，按照TileK=64设置，我们需要每次读两行。而在前面，我们已经把权重转换成ColMajor，那么意味着我们需要跨行去读，进而不连续，如图所示：

而这一步权重预处理操作，就是为了不连续的64 * 2 int8权重放到一块：

add_bias_and_interleave_int4s_inplace¶

这个就很简单了，就是把int8 / int4类型加个128 或 8，转换成unsigned类型

WeightOnly GEMV¶

在TRTLLM代码里，还有额外针对小bsz实现的Weightonly Kernel，不同的是其用的是CUDA Core进行计算。

Motivation: 

GEMM用TensorCore硬件通常对M维度有对齐要求，如m8表示M维度8对齐

如果M维没有满8，那么TensorCore会内部做padding去处理

考虑GEMV的场景，M=1，如果用TensorCore的话，我们相当于浪费了 1/8 的算力

因此我们使用CUDA Core去重写GEMV

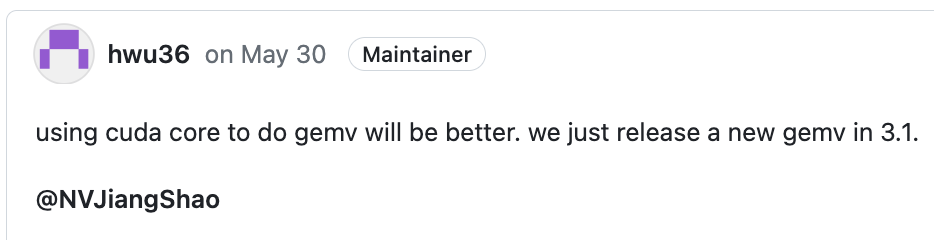
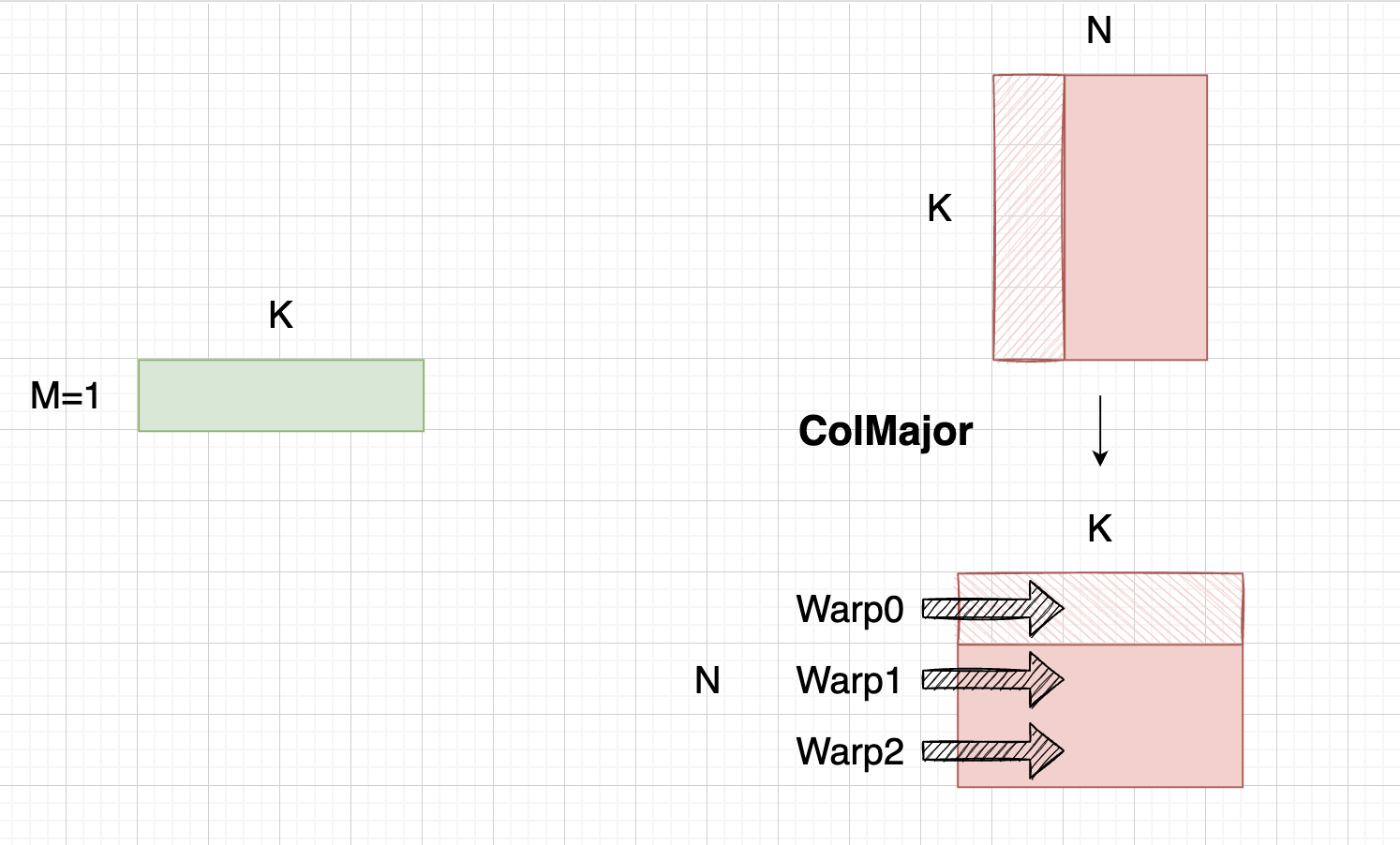
GEMV优化其实知乎一大堆，比GEMM简单，本质还是一个Warp处理一行或多行累加和（当然TRTLLM考虑了小batchsize下，不这么做了）

关于TRTLLM实现的一些小问题¶

在累加阶段，其用的是fp16累加，可能会有潜在的精度问题。

当然我也不确定在CUDA Core上到底有多少性能差距，或许是一种性能和精度的权衡？

计算卡如A100的TensorCore使用fp16还是fp32累加，其TFLOPS都是一样的：

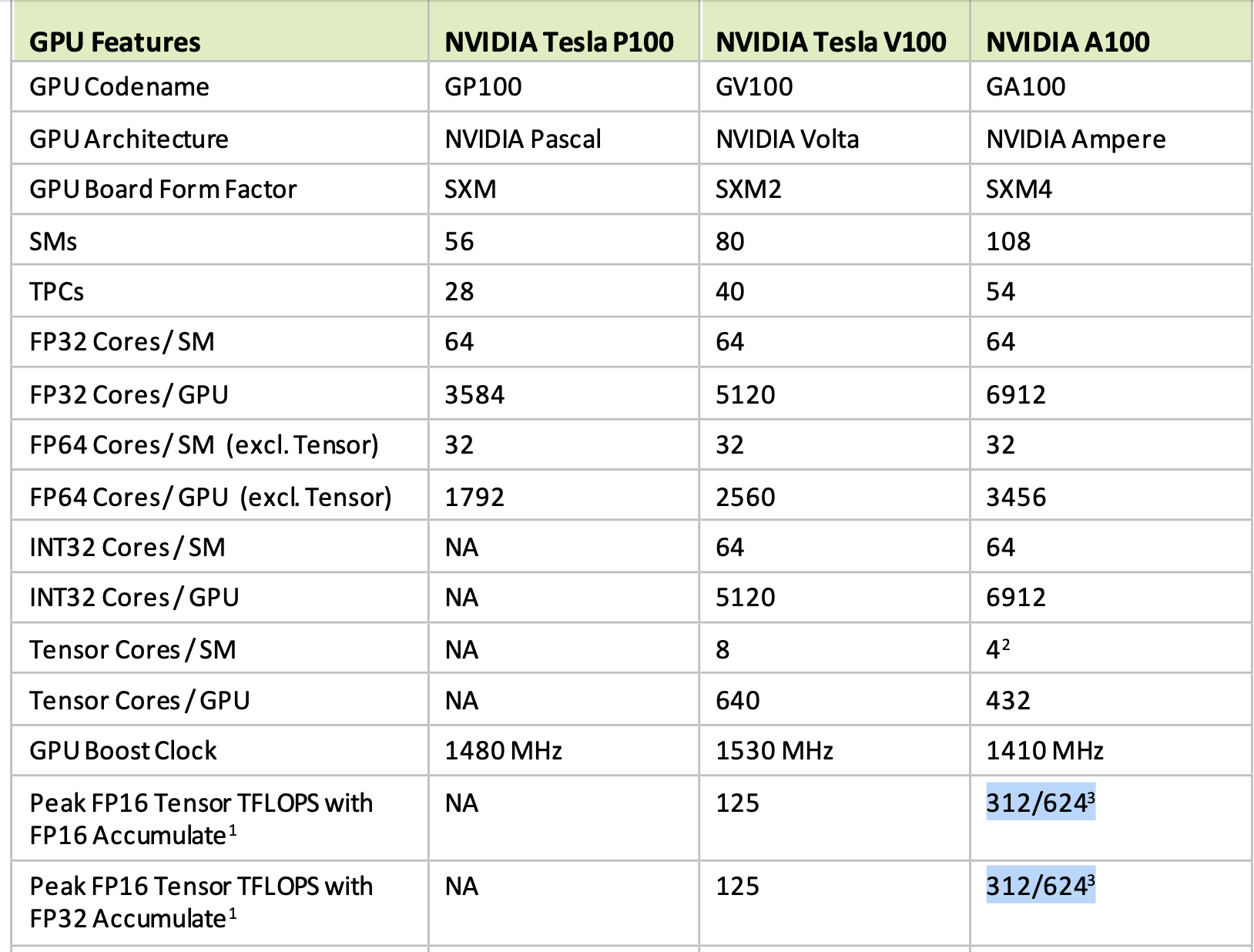
在一些游戏卡上有2x差距：

Volta架构支持¶

WeightOnly GEMM实现是支持Volta, Turing, Ampere三种架构的，而对应的变换也略有不同。

通过代码我们可以观察到有一个 TransformAfterLDG 和 TransformeAfterLDS。这表示int8转FP16是放到LoadGlobalMemory后做，还是LoadSharedMemory后做。

具体来说，是因为ldmatrix指令是从Turing架构后引入的，ldmatrix可以从SharedMemory直接加载满足TensorCore排布的数据，因此Turing/Ampere都是ldmatrix加载完成后做反量化操作。

而Volta没有这个指令，如果也要在LoadSharedMemory之后做，则需要重新写下shared memory的iterator，为了节省工作，对于Volta架构选择把反量化放在从GlobalMemory加载权重后做。

既然Volta不考虑用ldmatrix，那自然也就不需要 permute_B_rows_for_mixed_gemm 这个操作，所以权重预处理需要注意跳过这个操作。

启发式搜索¶

以下部分内容摘自NVIDIA的 streamK 论文（之前在高铁上其实写了一篇，但感觉理解不够深刻，就没有放出来）：

这个问题主要还是在讨论矩阵乘的最优分块策略，假设我们的GPU有4个SM，每个SM上可以运行1个threadBlock

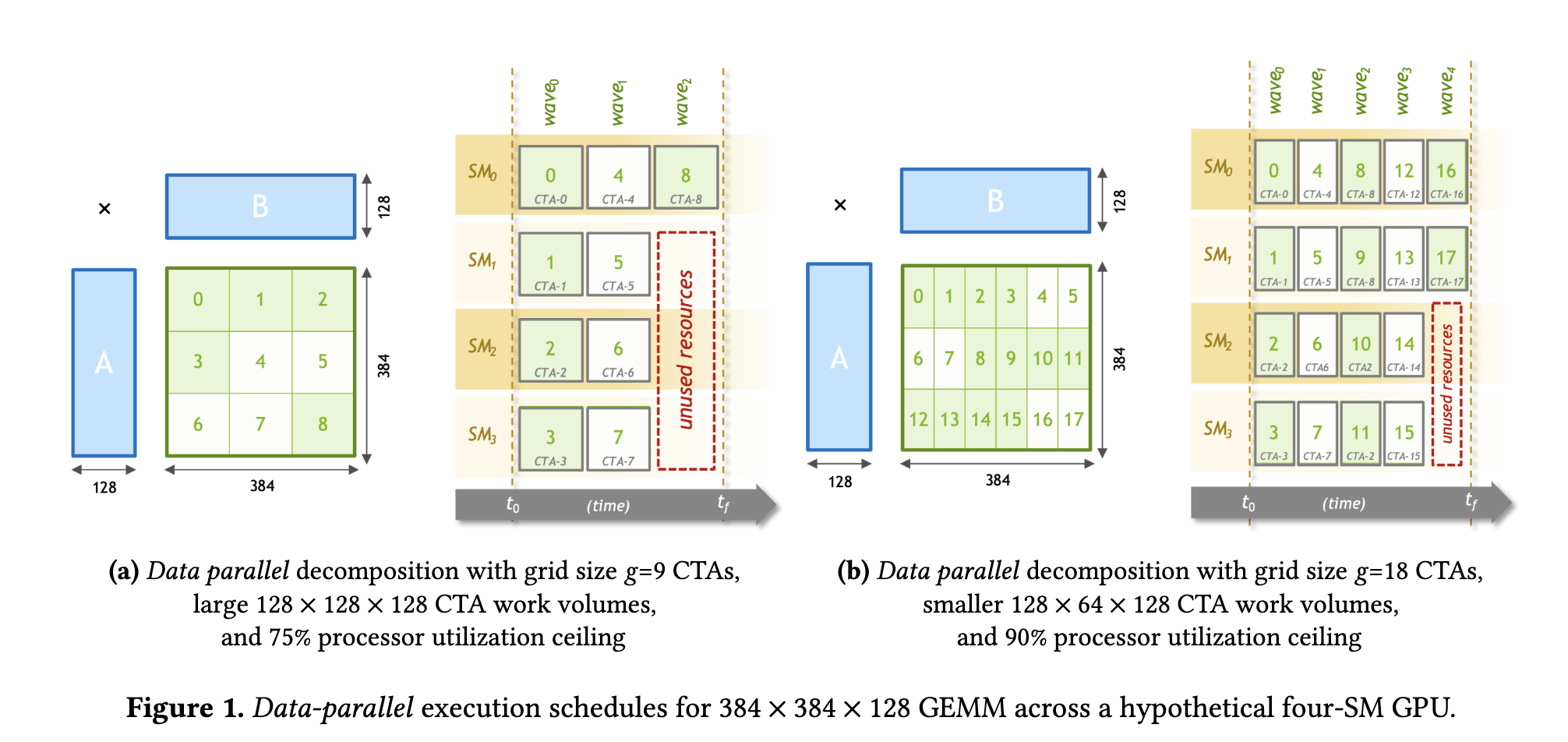
那么对于384x384x128的矩阵乘问题，如果我划分任务为一个block处理 128 * 128 * 128，那么一共需要9个CTA，此时需要3个完整的WAVE周期才能都执行完，并且第三个WAVE周期里，有3个SM是处于空闲状态，等待0号SM完成任务。利用率一共是 9 / (4 * 3) = 75%

而如果采用 128 * 64 * 128大小，则一共要18个CTA，需要5个完整的WAVE周期执行完，在最后一个WAVE周期里，有2个SM空闲。利用率是 18 / (4 * 5) = 90%