一文理解 PyTorch 中的 SyncBatchNorm¶

前言¶

我们知道在分布式数据并行多卡训练的时候，BatchNorm 的计算过程（统计均值和方差）在进程之间是独立的，也就是每个进程只能看到本地 GlobalBatchSize / NumGpu 大小的数据。

对于一般的视觉任务比如分类，分布式训练的时候，单卡的 batch size 也足够大了，所以不需要在计算过程中同步 batchnorm 的统计量，因为同步也会让训练效率下降。

但是对于一些模型占用显存很大，导致可以上的 batch size 很小这类任务来说，分布式训练的时候就需要用 SyncBatchNorm 来使得统计量更加的准确。

SyncBatchNorm 前向实现¶

前向第一步，计算本地均值和方差¶

假设在4张GPU上做分布式数据并行训练，我们来看下各个进程上 SyncBN 的行为：

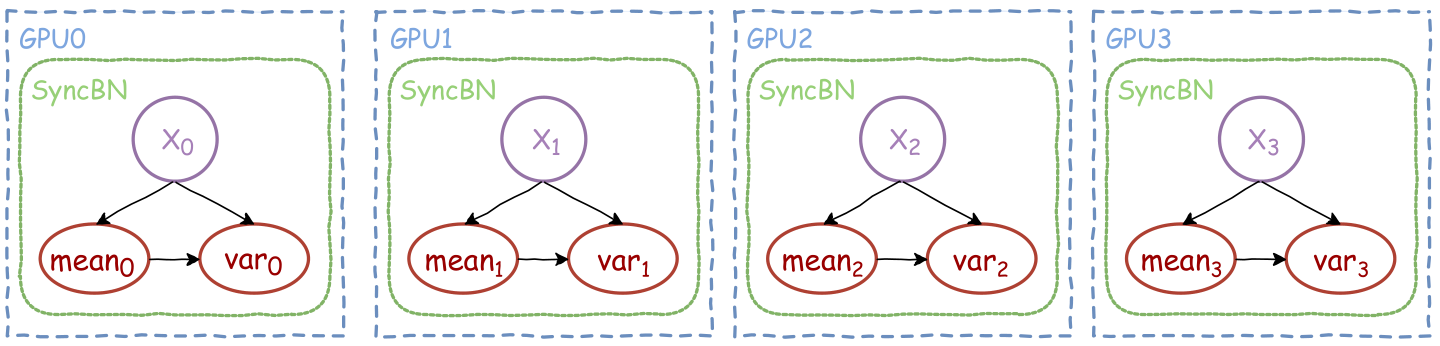
如上图所示，SyncBN前向实现的第一步是，每个GPU先单独计算各自本地数据 X_i 对应均值和方差（mean_i 和 var_i）。

而计算均值和方差的 CUDA kernel 具体实现是实现采用的 Welford迭代计算算法

https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Welford's_online_algorithm

我们知道传统方法计算均值，是要先把所有数据加起来然后再除以个数，而方差是在平均值的基础上做进一步的计算。

但是这样的计算方式有个问题是，在数据量非常之大的情况下，把所有数相加的结果是一个非常大的值，容易导致精度溢出。

而Welford迭代计算算法，则只需要对数据集进行单次遍历，然后根据迭代公式计算均值，可以避免传统算法可能导致的精度溢出的问题，且 Welford 算法可以并行化。

https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm

假设现在输入张量形状是 (B,C,H,W)，下面解释输入张量是 NCHW 格式的时候， CUDA kernel 具体开启线程的方式和每个线程具体计算细节。

由于线程的配置是按照固定的公式计算出来的，这里为了解释方便就固定为其中一种情况：

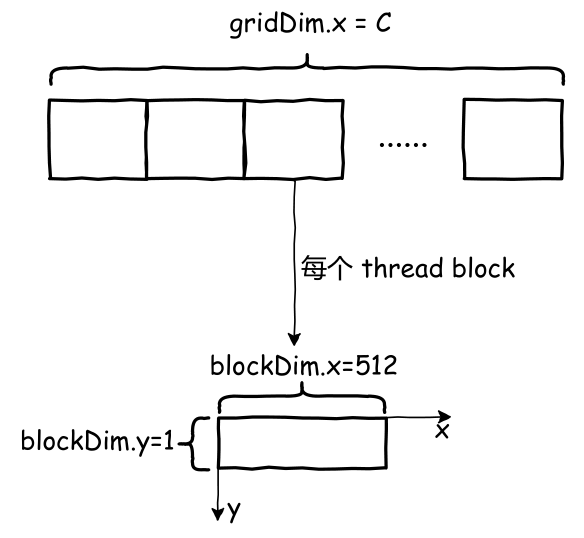
如上图所示，总共起了 C 个 thread block，也就是 grid 大小等于通道数。每个 thread block 负责计算某一个通道的均值和方差。

每个 thread block 的形状是两维，x维度是 512， y 维度是 1，共处理 B * H * W 大小的数据，其中数据组织形式是 x 方向是 H * W 维度，y 方向是 B 维度。

每个thread block 负责处理的数据大小和其中每个线程负责处理的位置，如下图所示：

如上图所示紫色方块表示thread block中的一个thread，紫色箭头指向表示，在kernel执行过程中，该线程所要负责处理的数据。

每个线程在x方向上每处理完一个数据，移动的步长为 blockDim.x=512，x方向遍历完之后，y方向移动步长为blockDim.y=1，以此类推。

kernel 执行的第一步就是，所有线程处理完自己所负责的数据，然后同步一下，接着就是合并每个线程计算得到的局部均值和方差。

而我们知道一个 thread block 内的线程，是按全局 id 顺序从0开始每 32 个线程分为一组，也就是一个 warp，然后以warp为单位来执行。

kernel 执行的第二步就是，每个 warp 内的线程合并均值和方差，通过 warp 级的同步元语库函数 __shfl_xor_sync 来实现 warp 内线程结果的合并。

这一步做完之后，warp 内每个线程都包含了合并之后的均值和方差，下面解释如何通过 __shfl_xor_sync 来实现 warp 内线程结果合并的：

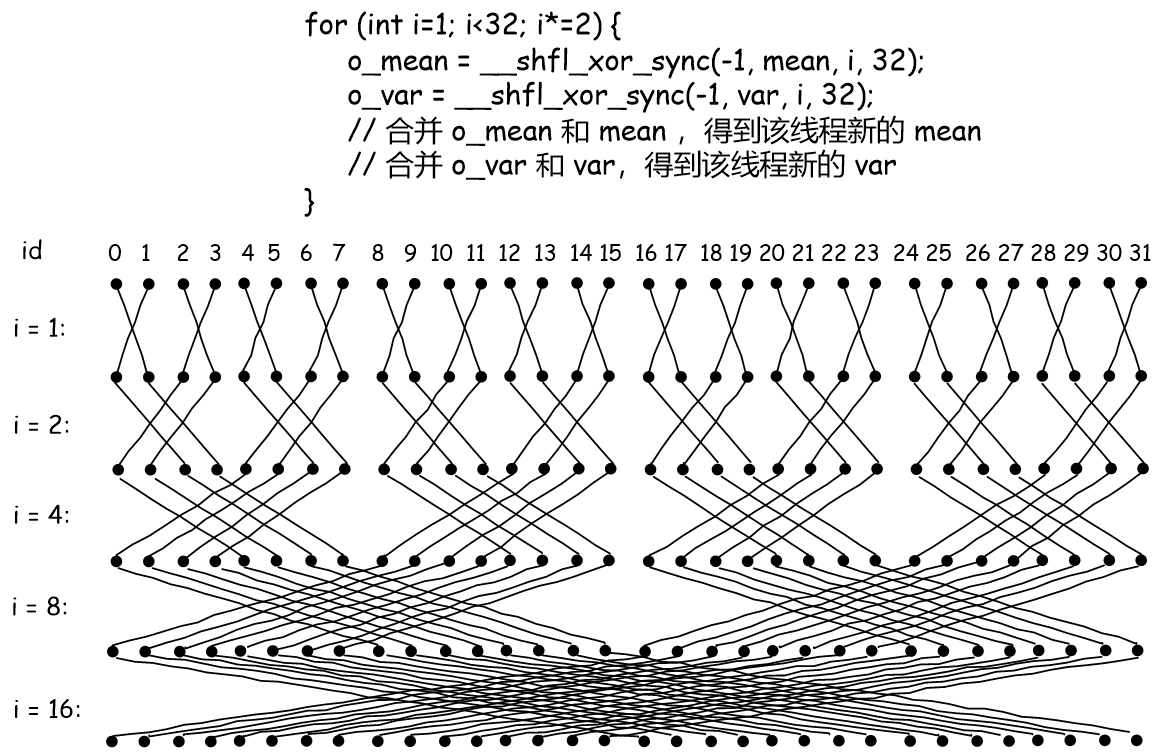
上图中的每一行的32个黑点表示一个 warp 内的32个线程，上方的id 表示每个线程在warp内的id。

然后我们看合并 mean 和 var 的循环，这里可视化了每个循环内线程之间的交互。

__shfl_xor_sync 简单来理解，只需要关注第 2 和 3 个参数，第二个参数是线程之间要交换的值，第三个参数传 i。

具体作用就是，当前线程的 id 和这个 i 做异或 xor 位运算，计算得到的结果也是 id ，也就是当前线程要与哪个线程交换值。

当 i = 1 的时候，

对于线程 id 0 和 1， 0 xor 1 = 1 ， 1 xor 1 = 0，则就是线程 0 和 1 交换各自的均值和方差，然后就都持有了合并之后的均值和方差了。

再看线程 id 2 和 3， 2 xor 1 = 3 ，3 oxr 1 = 2，所以 2 和 3 交换。

同理可得第一轮循环，是线程按顺序2个为一组组内合并。

当 i = 2 的时候，

对于线程 id 0 和 2， 0 xor 2 = 2 ， 2 xor 2 = 0，

对于线程 id 1 和 3，1 xor 2 = 3， 3 xor 2 = 1

所以交换完合并之后，thread 0 ~ 3 就都持有了这4个线程合并之后的均值和方差了。

同理可得，

i = 2 的时候线程按顺序4个为一组，组内根据异或运算计算交换线程对合并均值和方差。

i = 4 的时候，线程按顺序8个为一组，

i = 8 的时候，线程按顺序16个为一组，

当最后一轮 i = 16 循环完了之后，warp 内每个线程就都持有了该 warp 的所有线程合并的均值和方差了。

kernel 执行的最后一步是，上面每个 warp 内结果合并完，会做一次全局的线程同步。之后再将所有 warp 的结果合并就得到该 thread block 所负责计算的通道均值和方差了。

前向第二步，GPU之间同步均值和方差¶

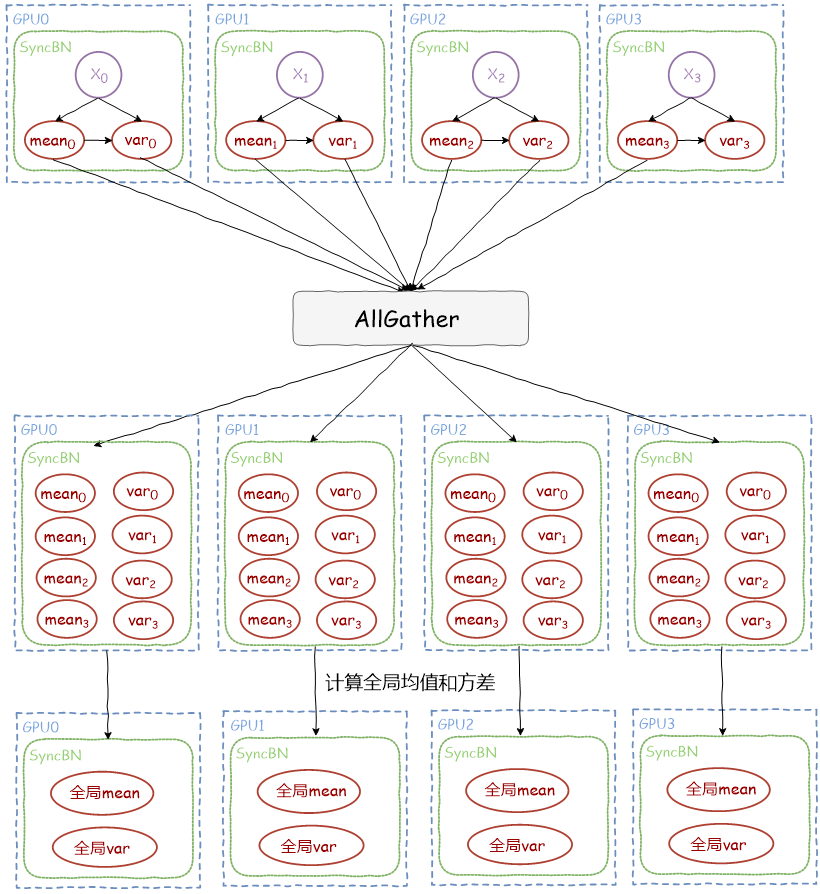
通过集合通信操作 AllGather 让每个 GPU 上的进程都拿到所有 GPU 上的均值和方差，最后就是每个GPU内计算得到全局的均值和方差，同时更新 running_mean 和 running_var

前向第三步，计算 SyncBN 的输出¶

最后这一步就一个常规的batchnorm操作，对输入 x 做 normalize 操作得到输出，cuda kernel 就是一个 eltwise 的操作，因为不需要计算均值和方差了。这里就不展开了，有兴趣的读者可以看文末的参考链接，去阅读torch的源码，也可以学习一下对于 NHWC格式的 cuda kernel 是如何实现的。

SyncBatchNorm 反向实现细节¶

BatchNorm 反向计算公式¶

首先复习一下 BatchNorm 反向，输入格式是 (B,C,H,W)

则某个通道（通道索引 c）对应的输入 x 、weight 和 bias 梯度计算公式，这里不做推导只列出公式：

前置公式：

输出梯度为 y_grad

$inv\_std\_c = \frac{1}{\sqrt{var[c] + eps}}$

$sum\_dy = \sum_{b=0}^{B-1}\sum_{h=0}^{H-1}\sum_{w=0}^{W-1}(y\_grad[b][c][h][w])$

$sum\_dy\_xmu = \sum_{b=0}^{B-1}\sum_{h=0}^{H-1}\sum_{w=0}^{W-1}(x[b][c][h][w] - mean[c]) * y\_grad[b][c][h][w]$

weight 对应通道 c 的梯度：

$weight\_grad[c] = sum\_dy\_xmu * inv\_std\_c$

bias 对应通道 c 的梯度：

$bias\_grad[c] = sum\_dy$

输入 x 对应通道 c 上某个位置 b， h， w 的梯度：

$rc=B*H*W$

$k = \frac{(sum\_dy\_xmu * inv\_std\_c * inv\_std\_c)}{rc}$

$iw = weight[c] * inv\_std\_c$

$g\_mean\_c = \frac{sum\_dy}{rc}$

$x\_grad[b][c][h][w]$

$=(y\_grad[b][c][h][w] - g\_mean\_c - (x[b][c][h][w] - mean[c])*k)*iw$

反向计算流程¶

每个GPU都计算出本地对应的 weight_grad ，bias_grad ，sum_dy 和 sum_dy_xmu，具体CUDA kernel 实现思路和前向第一步类似，这里就不展开了，有兴趣可以去阅读源码。

由于分布式数据并行下，权值的梯度会自动做全局同步，所以 SyncBN 就不需要管权值梯度的跨 GPU 的同步。

而对于sum_dy 和 sum_dy_xmu，则通过集合通信操作 AllReduce 将所有GPU上的结果累加，使得每个GPU上持有全局累加的结果。

最后每个 GPU 根据上面的计算公式计算本地输入x对应的梯度，但是需要注意的是，由于 sum_dy 和 sum_dy_xmu是跨 GPU 全局累加的结果，所以上面公式中的 rc=B*H*W要改为 rc=B*H*W*num_gpu 。该 CUDA kernel 的实现，根据上述公式，也是一个 eltiwse 的操作，细节可以去阅读torch源码。

参考资料¶

本文总阅读量次